Лекция 8 MathCAD. Матрицы – продолжение. Условны функции. Нелинейные уравнения и системы уравнений
Создание матриц специального вида
Для создания матрцы специального вида в MathCAD существуют встроенные функции (Рис. 1). identity(N) - создает единичную матрицу размера NхN;

 diag(v) - создает диагональную матрицу, на диагонали которой находятся элементы вектора v;
diag(v) - создает диагональную матрицу, на диагонали которой находятся элементы вектора v;
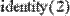


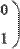
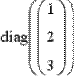
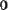

 Рис. 1. Создание матриц специального вида.
Рис. 1. Создание матриц специального вида.
Слияние и разбиение матриц
Из матрицы или вектора можно выделить либо отдельный элемент, либо вектор-столбец, либо подматрицу. И обратно, можно "склеить" несколько матриц в одну.
Выделение частей матрицы


 Для выделения отдельного элемента предназначен оператор нижнего индекса (Рис. 2.).
Для выделения отдельного элемента предназначен оператор нижнего индекса (Рис. 2.).
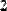
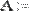

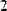

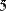


 Рис. 2. Выделение одного элемента матрицы.
Рис. 2. Выделение одного элемента матрицы.
 Выделить столбец из матрицы можно нажатием кнопки (Matrix Column) на панели Matrix
Выделить столбец из матрицы можно нажатием кнопки (Matrix Column) на панели Matrix
 á ñ
á ñ
 или сочетанием клавиш <Ctrl>+<6> на клавиатуре. В результате получим оператор вида .
или сочетанием клавиш <Ctrl>+<6> на клавиатуре. В результате получим оператор вида .
Этот оператор называют еще оператором верхнего индекса. В местозаполнителях указывается имя матрицы и индекс выделяемого столбца(Рис. 3.).
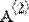


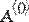


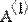

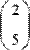
Рис. 3 Выделение одного столбца матрицы.
Лекция 9 36
Чтобы выделить из матрицы строку, нужно применить тот же оператор верхнего индекса к транспонированной матрице (Рис. 4).
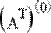

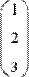
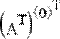

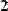
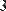
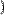
Рис. 4 Выделение одной строки матрицы.

 Для выделения подматрицы нужно использовать встроенную функцию submatrix(A,ir,jr,ic,jc), возвращающую часть матрицы А, находящуюся между строками ir, jr и столбцами ic, jc включительно (Рис. 5).
Для выделения подматрицы нужно использовать встроенную функцию submatrix(A,ir,jr,ic,jc), возвращающую часть матрицы А, находящуюся между строками ir, jr и столбцами ic, jc включительно (Рис. 5).
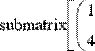
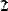
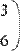
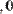
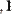
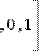

 Рис.5. Выделение подматрицы.
Рис.5. Выделение подматрицы.






 С помощью функции submatrix( ) можно выделить из матрицы одну строку (Рис. 6.) или один столбец (Рис. 7).
С помощью функции submatrix( ) можно выделить из матрицы одну строку (Рис. 6.) или один столбец (Рис. 7).
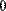

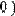
 Рис. 6. Выделение строки с помощью функции submatrix( ).
Рис. 6. Выделение строки с помощью функции submatrix( ).
éæ1 3 5 ö
ù æ 3 ö
submatrix
êç 2 4
8 ÷ , 0 , 2 , 1 , 1ú
= ç 4 ÷
êç ÷
ú ç ÷
ëè9 0 7 ø
û è 0 ø
Рис. 7. Выделение столбца с помощью функции submatrix( ).
Операцией верхнего индекса и функцией submatrix( ) можно выделять части из матриц- векторов и матриц-строк (Рис. 8.) Следует помнить только, что размер их составляет Nх1 и 1хN, соответственно (Рис. 8).
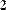
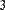
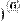

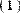
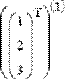

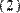
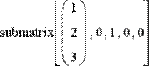


Лекция 9 37
submatrix[( 9 0 7 ) , 0, 0, 0, 1] = ( 9 0 )
Рис. 8. Выделение частей из векторов и строк.
Слияние матриц
Для того чтобы составить из двух или более матриц одну, в MathCAD предусмотрены две матричные функции (Рис. 10):
- функция augment (А, В, С,...) - возвращает матрицу, сформированную слиянием матриц-аргументов слева направо;
- функция stack (А, В, С,...) - возвращает матрицу, сформированную слиянием матриц- аргументов сверху вниз;














 А,В,С,... — векторы или матрицы соответствующего размера.
А,В,С,... — векторы или матрицы соответствующего размера.
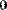
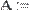
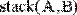

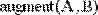

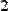
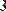
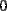
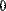
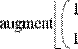



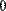














 Рис. 10. Примеры слияния матриц.
Рис. 10. Примеры слияния матриц.
Вывод размера матриц
Для получения сведений о размерах матриц или векторов предусмотрены следующие встроенные функции (Рис. 11):
-  rows(A) - число строк;
rows(A) - число строк;
- cols(A) - число столбцов;
- length(v) - число элементов вектора;
- last(v) - индекс последнего элемента вектора;
Здесь А - матрица или вектор;
v - вектор.
Число элементов вектора length(v) и индекс его последнего элемента last(v) совпадают, если индексы нумеруются с 1, т. е. системная константа ORIGIN равна 1.
Лекция 9 38
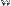
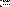
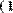
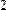
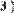
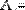
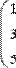
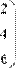

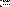
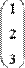
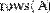

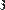
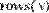

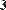
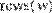

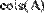

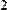
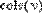

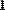
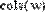

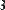
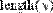

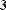
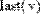

Рис. 11. Размер матриц и векторов.
Функции сортировки матриц и векторов
Рассмотрим функции сортировки, приняв следующие обозначения: v – вектор; А –
матрица; i – индекс строки или столбца.
Сортировка векторов:
- sort(v) — сортировка элементов вектора в порядке возрастания (Рис.12.);
- reverse(v) — перестановка элементов вектора в обратном порядке (Рис. 12);


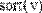

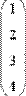
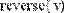


Рис. 12. Сортировка векторов.
Сортировка матриц по столбцу:
- csort(A,i) — перестановка строк матрицы сортировкой элементов i-го столбца по возрастанию (Рис. 13).
æ 1 csort (A , 0) = ç 2
ç
è 3
æ 1 9 ö
A := ç 3 0 ÷
ç ÷
è 2 8 ø
9 ö
8 ÷
÷
0 ø
æ 3 0 öcsort (A , 1) = ç 2 8 ÷
ç ÷
è 1 9 ø
Рис. 13. Сортировка матриц по столбцу.
Сортировка матриц по строке:
Лекция 9 39
- rsort(A,i) — перестановка столбцов матрицы сортировкой элементов i-й строки по возрастанию (Рис. 14).
æ 1 9 örsort(A, 0) = ç 3 0 ÷
ç ÷
è 2 8 ø
æ 9 1 örsort(A , 1) = ç 0 3 ÷
ç ÷
è 8 2 ø
æ 1 9 örsort(A, 2) = ç 3 0 ÷
ç ÷
è 2 8 ø
Рис. 14. Сортировка матриц по строке.

Дата добавления: 2014-12-24; просмотров: 1934;
