E.2.2. Матрицы
1.Даны целые числа а1, а2, а3. Получить целочисленную матрицу 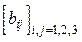 , для которой bij= ai-3aj.
, для которой bij= ai-3aj.
2. Даны действительные числа а1, ... , а10, b1, ... , b20. Получить действительную матрицу 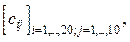 для которой
для которой 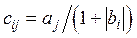 .
.
3. Получить целочисленную матрицу 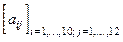 , для которой aij=i+2j.
, для которой aij=i+2j.
4.Дано натуральное число n. Получить действительную матрицу 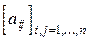 , для которой
, для которой
а) 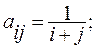 б)
б) 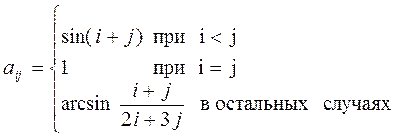
5.Дана действительная квадратная матрица 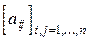 . Получить две квадратные матрицы
. Получить две квадратные матрицы 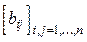 ,
, 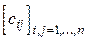 , для которых
, для которых
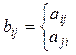
| при 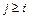 в оставшихся случаях
в оставшихся случаях
| 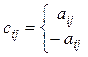
| при 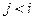 в оставшихся случаях
в оставшихся случаях
|
6.Получить действительную матрицу 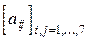 , первая строка которой задается формулой
, первая строка которой задается формулой 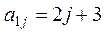 (
( 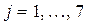 ), вторая строка задается формулой
), вторая строка задается формулой 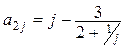 (j=1, ... ,7), а каждая следующая строка есть сумма двух предыдущих.
(j=1, ... ,7), а каждая следующая строка есть сумма двух предыдущих.
7.Дано натуральное число n, действительная матрица размера 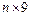 . Найти среднее арифметическое:
. Найти среднее арифметическое:
| а) каждого из столбцов; |
| б) каждого из столбцов, имеющих четные номера. |
8.Дано натуральное число n. Выяснить, сколько положительных элементов содержит матрица 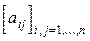 , если
, если
а) 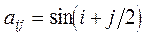 ; ;
| б) 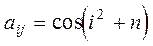 ; ;
| в) 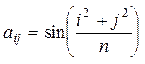 . .
|
9. Дана действительная квадратная матрица размера n´m, в которой не все элементы равны нулю. Получить новую матрицу путем деления всех элементов данной матрицы на ее наибольший по модулю элемент.
10.Даны натуральное число m, целые числа a1, ... , am и целочисленная квадратная матрица порядка m. Строку с номером i матрицы назовем отмеченной, если ai >0, и неотмеченной - в противном случае.
а) Нужно все элементы, расположенные в отмеченных строках матрицы, преобразовать по правилу: отрицательные элементы заменить на -1, положительные - на 1, а нулевые оставить без изменения.
б) Подсчитать число отрицательных элементов матрицы, расположенных в отмеченных строках.
11. Дана действительная квадратная матрица порядка 12. Заменить нулями все элементы, расположенные на главной диагонали и выше нее.
12. Даны действительные числа x1, ..., x8. Получить действительную квадратную матрицу порядка 8:
а) 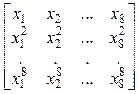 ; ;
| б) 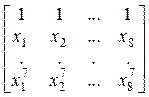
|
13. Дана действительная квадратная матрица размера n´m.Определить числа b1, ... ,bm , равные соответственно:
а) суммам элементов строк;
б) произведениям элементов строк;
в) наименьшим значениям элементов строк;
г) значениям средних арифметических элементов строк;
д) разностям наибольших и наименьших значений элементов строк.
14. Даны натуральное число n, действительная матрица 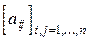 . Получить последовательность элементов главной диагонали a11, a22, ... , ann.
. Получить последовательность элементов главной диагонали a11, a22, ... , ann.
15.Все элементы с наибольшим значением в данной целочисленной квадратной матрице порядка 10 заменить нулями.
16.Дана действительная квадратная матрица размера 6´9. Найти среднее арифметическое наибольшего и наименьшего значений ее элементов.
17.Дана действительная квадратная матрица размера 18´n. Найти значение наибольшего по модулю элемента с найденным значением модуля.
18. Дана действительная квадратная матрица размера n´m. Найти сумму наибольших значений элементов ее строк.
19. В данной действительной квадратной матрице порядка n найти сумму элементов строки, в которой расположен элемент с наименьшим значением. Предполагается, что такой элемент единственный.
20. В данной действительной квадратной матрице размера 6´9 поменять местами строку, содержащую элемент с наибольшим значением, со строкой, содержащей элемент с наименьшим значением. Предполагается, что эти элементы единственны.
21. Даны натуральное число и квадратная матрица порядка n, действительные a1, ... , an+5 . Элементы последовательности домножить на 10, если наибольший элемент матрицы (в предположении, что такой элемент единственный) находятся на главной диагонали, и на 0.5 в противном случае.
22.В данной квадратной целочисленной матрице порядка 17 указать индексы всех элементов с наибольшим значением.
23.Дана действительная квадратная матрица размера n´m , все элементы которой различны. В каждой строке выбирается элемент с наименьшим значением, затем среди этих чисел выбирается наибольшее. Указать индексы элемента с найденным значением.
24.Дана действительная квадратная матрица размера n´m . Получить последовательность b1, ... , bn, где bk – это:
а) наибольшее из значений элементов k-й строки;
б) сумма из наибольшего и наименьшего из значений элементов k-й строки;
в) число отрицательных элементов k-й строки;
г) произведение квадратов тех элементов k-й строки, модули которых принадлежат отрезку [1, 1.5].
25.Даны натуральное число n, целочисленная матрица 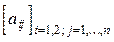 . Найти сумму тех из элементов a2j (j=1, ... , n), для которых a1j имеет значение наибольшего среди значений a11, a12, ... , a1m.
. Найти сумму тех из элементов a2j (j=1, ... , n), для которых a1j имеет значение наибольшего среди значений a11, a12, ... , a1m.
26. Дана целочисленная квадратная матрица порядка 8. Найти наименьшее из значений элементов столбца, который обладает наибольшей суммой модулей элементов. Если таких столбцов несколько, то взять первый из них.
27. Даны натуральное число n, целочисленная квадратная матрица порядка n. Получить b1, ... , bn, где bi – это:
а) наименьшее из значений элементов, находящихся в начале i-й строки матрицы до элемента, принадлежащего главной диагонали, включительно;
б) значение первого по порядку положительного элемента i-й строки (если таких элементов нет, то принять bi=1);
в) сумма элементов, расположенных за первым отрицательным элементом в i-й строке (если все элементы строки не отрицательны, то принять bi=1);
г) сумма элементов, предшествующих последнему отрицательному элементу i-й строки (если все элементы строки не отрицательны, то принять bi=1)
28.Дана целочисленная квадратная матрица порядка n. Найти номера строк:
а) все элементы которых - нули;
б) элементы каждой из которых одинаковы;
в) все элементы которых четны;
г) элементы каждой из которых образуют монотонную последовательность (монотонно убывающую или монотонно возрастающую);
д) элементы которых образуют симметрические последовательности (палиндромы).
29.Даны натуральное число n, действительное число x, действительная матрица размера n´2n. Получить последовательность b1, ... , bn из нулей и единиц, где bi =1, если элементы i-й строки матрицы не превосходит x, и bi =0 в противном случае.
30.Дана действительная квадратная матрица порядка n. Построить последовательность действительных чисел a1, ..., an по правилу: если в i-й строке матрицы элемент, принадлежащий главной диагонали, отрицателен, то ai равно сумме элементов i-й строки, предшествующих первому отрицательному элементу; в противном случае ai равно сумме последних элементов i-й строки, начинающихся с первого по порядку неотрицательного элемента.
31.Дана действительная квадратная матрица порядка 10. В строках с отрицательным элементом на главной диагонали найти:
| а) сумму всех элементов; |
| б) наибольший из всех элементов. |
32. Дана действительная квадратная матрица порядка n. Рассмотрим те элементы, которые расположены в строках, начинающихся с отрицательного элемента. Найти сумму тех из них, которые расположены соответственно ниже, выше и на главной диагонали.
33. Дана действительная квадратная матрица порядка 9. Получить целочисленную квадратную матрицу того же порядка, в которой элемент равен единице, если соответствующий ему элемент исходной матрицы больше элемента, расположенного в его строке на главной диагонали, и равен нулю в противном случае.
34.Дана действительная квадратная матрица порядка n. Получить x1x2+ + 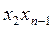 +...+xnx1, где xk - наибольшее значение элементов k-й строки данной матрицы.
+...+xnx1, где xk - наибольшее значение элементов k-й строки данной матрицы.
35. Даны действительная квадратная матрица порядка n, натуральные числа i, j (1£i£n, 1£j£n). Из матрицы удалить i-ю строку и j-й столбец.
36. Даны натуральное число 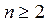 , действительная квадратная матрица порядка n. Построить последовательность b1, ..., bn из нулей и единиц, в которой bi= 1 тогда и только тогда, когда:
, действительная квадратная матрица порядка n. Построить последовательность b1, ..., bn из нулей и единиц, в которой bi= 1 тогда и только тогда, когда:
а) элементы i-й строки матрицы образуют возрастающую последовательность;
б) элементы i-й строки матрицы образуют возрастающую или убывающую последовательность.
37. Дана целочисленная квадратная матрица порядка 15. Выяснить, имеются ли в матрице ненулевые элементы, и если имеются, то указать индексы:
| а) одного из ненулевых элементов; |
| б) всех ненулевых элементов. |
38.Даны натуральные числа i, j, действительная матрица размера 18´24 (1£i<j£24). Поменять в матрице местами i-й и j-й столбцы.
39.Даны натуральное число n, действительная квадратная матрица порядка n. Построить последовательность b1, ..., bn из нулей и единиц, в которой bi=1 тогда и только тогда, когда в i-й строке матрицы есть хотя бы один отрицательный элемент.
40.С помощью 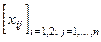 - действительной матрицы на плоскости задано n точек так, что x1j, x2j - координаты j-й точки. Точки попарно соединены отрезками. Найти длину наибольшего отрезка.
- действительной матрицы на плоскости задано n точек так, что x1j, x2j - координаты j-й точки. Точки попарно соединены отрезками. Найти длину наибольшего отрезка.
41.Даны натуральные числа n и m, действительное число r, действительная матрица размера n´m. Получить значение b1rn-1 +b2 rn-2 +...+bn,где bk - первый по порядку положительный элемент в k-й строке матрицы (k=1, ..., N); если в k-й строке нет положительных элементов, то bk= 0.5.
42.Найти сумму квадратов тех элементов aij матрицы 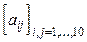 , для которых выполнено 2£i£9, 2£j£9,
, для которых выполнено 2£i£9, 2£j£9, 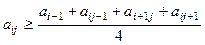 .
.
43.Дана действительная квадратная матрица порядка 9. Вычислить сумму тех из ее элементов, расположенных на главной диагонали и выше нее, которые превосходят по величине все элементы, расположенные ниже главной диагонали. Если на главной диагонали и выше нее нет элементов с указанным свойством, то ответом должно служить сообщение об этом.
44. Дана целочисленная матрица 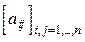 . Получить b1, ... ,bn, где bi- это
. Получить b1, ... ,bn, где bi- это
а) 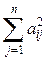 ; ;
| б) 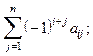
| в) 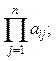
| г) 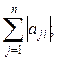
|
д) 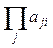 для всех таких j, что 1<aji£n; для всех таких j, что 1<aji£n;
| |||
е) 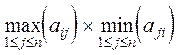 . .
|
45.Будем называть соседями элемента с индексами i, j некоторой матрицы такие элементы этой матрицы, соответствующие индексы которых отличаются от i и j не более, чем на единицу. Для данной целочисленной матрицы 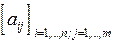 найти матрицу из нулей и единиц
найти матрицу из нулей и единиц 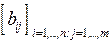 , элемент которой bij равен единице, когда:
, элемент которой bij равен единице, когда:
| а) все соседи aij меньше самого aij ; |
| б) все соседи aij и само aij равны нулю; |
| в) среди соседей aij есть не менее двух совпадающих с aij. |
46.Даны две целочисленные квадратные матрицы порядка 6. Найти последовательность из нулей и единиц b1..., b6 такую, что bi , когда:
а) все элементы i-й строки первой матрицы больше соответствующих элементов i-й строки второй матрицы;
б) все элементы i-х строк первой и второй матриц отрицательны;
в) i-е строки первой и второй матриц содержат вместе не более трех положительных элементов;
г) количество отрицательных и неотрицательных элементов i-й строки первой матрицы совпадает соответственно с количеством отрицательных и неотрицательных элементов i-й строки второй матрицы.
47.Таблица футбольного чемпионата задана квадратной матрицей порядка n, в которой все элементы, принадлежащие главной диагонали, равны нулю, а каждый элемент, не принадлежащий главной диагонали, равен 2,1 или 0 (числу очков, набранных в игре: 2 - выигрыш, 1 - ничья, 0 - проигрыш).
а) Найти число команд, имеющих больше побед, чем поражений.
б) Определить номера команд, прошедших чемпионат без поражений.
в) Выяснить, имеется ли хотя бы одна команда, выигравшая более половины игр.
48. Даны натуральные числа x1, y1, ..., xn, yn. Числа xi, yi рассматриваются как координаты i-й точки (i=1, ..., n). Обозначим через rij расстояние от i-й точки до j-й. Получить на экране заданные точки и соединить отрезком i-ю точку с j-й в том случае, если выполняется по крайней мере одно условие:
1) rij имеет наибольшее значение из ri1 ri2 , ..., rin;
2) rij имеет наибольшее значение ri1 ri2 , ..., rin;.
49.Дана целочисленная квадратная матрица порядка n. Каждый элемент матрицы ставится в соответствие точке, принадлежащей квадратной области экрана размером n´m точек. Левый верхний угол области имеет координаты (0, 0). Соответствие между элементами матрицы и точками области экрана устанавливается следующим образом: элемент матрицы, стоящий в строке с номером i и в столбце с номером j, соответствует точке экрана, находящейся на пересечении строки точек области с номером i и столбца точек области с номером j. Полагая, что каждый элемент матрицы задает цвет соответствующей точки экрана, получить на экране изображение, закодированное в матрице А.
50.Даны две целочисленные квадратные матрицы порядка n. В каждой из матриц закодировано изображение прямоугольной области экрана размером n´n точек с координатами левого верхнего угла (0, 0) (см. предыдущую задачу). В отличие от предыдущей задачи, все элементы обеих матриц - это числа, равные 0, если точка составляет фон, или 1, если точка - часть изображения. Получить на экране изображение, являющееся:
а) пересечением изображений, закодированных в первой и второй матрицах;
б) объединением изображений, закодированных в первой и второй матрицах.
51.Даны натуральные числа x1, y1, ..., xn, yn , целочисленная матрица 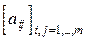 . Последовательность x1, y1, ... , xn, yn задает координаты n точек. Матрица указывает, как соединены между собой точки: aij= 1, если i-я точка соединена с j-й, и aij= 0 в противном случае (aij= aji). Получить на экране точки, заданные последовательностью x1, y1, ..., xn, yn, и соединить их между собой так, как указано в данной матрице.
. Последовательность x1, y1, ... , xn, yn задает координаты n точек. Матрица указывает, как соединены между собой точки: aij= 1, если i-я точка соединена с j-й, и aij= 0 в противном случае (aij= aji). Получить на экране точки, заданные последовательностью x1, y1, ..., xn, yn, и соединить их между собой так, как указано в данной матрице.
52.Пусть a1, a2, ... - последовательность квадратных матриц из нулей и единиц такая, что порядок матрицы ai равен 3i и
1) 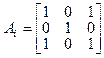
| 2) при i>1 имеет место  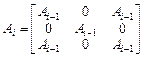 , ,
|
где 0 обозначает часть матрицы, заполненную нулями.
Дано натуральное число n. Построить изображение квадратной области экрана, закодированное в матрице An. Левый верхний угол области должен совпадать с левым верхним углом экрана. Опробовать различные способы использования цвета при построении изображения. Если фоновый цвет имеет номер 0, а остальные цвета - номера 1, ..., k, то при обработке элемента Aij не равного 0 можно, например, брать цвет с номером L+1, где L равно остатку от деления: i2+ j3 на k, и т.д.
53.Дана символьная квадратная матрица порядка 10. Заменить буквой a все ее элементы, расположенные выше главной диагонали.
54.Даны натуральное n, символьная квадратная матрица порядка n. Получить последовательность b1 , ..., bn из нулей и единиц, в которой bi= 1 тогда и только тогда, когда в i-й строке число символов * не меньше числа пробелов.
55.Дана символьная матрица размера 13´18. Найти:
а) номер первой по порядку строки, содержащий наибольшее число цифр;
б) номер первого по порядку столбца, содержащего наименьшее число пробелов на пересечении со строками, номера которых четны;
в) номер последней по порядку строки, содержащей наибольшее количество букв ш, щ;
г) номер последнего по порядку столбца, в котором содержится наибольшее количество попарно различных символов.
56.При перепечатке текста на пишущей машинке часто получается так, что в конце строки остается несколько неиспользованных позиций. Число неиспользованных позиций меняется от строки к строке, и поэтому правый край отпечатанного текста получается неровным. Типографский набор дает ровный правый край, в частности, за счет увеличения промежутков между словами, встречающимися в строке.
Предлагается задача выбора подходящих промежутков. Дана символьная матрица n´m, в каждой из строк которой имеется по крайней мере один пробел, за которым следует отличный от пробела символ (т.е. имеется по крайней мере одна группа пробелов внутри строки). За счет изменения групп пробелов внутри строк надо добиться того, чтобы в конце каждой из строк пробелы отсутствовали. Количества пробелов в разных группах, располагающихся внутри одной и той же строки, должны различаться не более чем на единицу.
57. Дана действительная квадратная матрица порядка n.
а) Найти сумму элементов первого столбца.
б) Найти сумму элементов главной и побочной диагоналей.
в) Найти наибольшее из значений элементов первой и последней строк.
г) Найти наименьшее из значений элементов побочной диагонали и двух соседних с ней линий.
д) Для данного натурального m ( 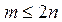 ) найти сумму тех элементов матрицы, сумма индексов которых равна m.
) найти сумму тех элементов матрицы, сумма индексов которых равна m.
е) Выяснить, верно ли, что наибольшее из значений элементов главной диагонали больше, чем наименьшее из значений элементов побочной диагонали.
Дата добавления: 2014-12-24; просмотров: 5619;
