Векторы и матрицы
Кроме ранжированных переменных (массивов, элементы которых зависят от их индекса) в
MathCAD присутствует 2-й тип массивов:
- векторы (одноиндексные или одномерные массивы),
- матрицы (двухиндексные или двумерные массивы),
- тензоры (многоиндексные или многомерные массивы);
Для второго типа массивов – векторов, матриц и тензоров значения их элементов могут зависеть от их индексов, или могут быть никак не связаны с индексами
.
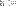
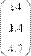

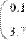
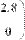




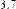

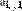


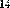

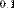
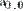 Рис. 18. Одномерный массив (вектор) Рис. 19. Двумерный массив (матрица)
Рис. 18. Одномерный массив (вектор) Рис. 19. Двумерный массив (матрица)
Доступ к элементам массива
Доступ ко всему массиву осуществляется по его имени.
Например, если напечатать"а = " , то на экран выводится соответствующий вектор (Рис. 18) или матрица
(Рис. 19).
Доступ к отдельному элементу массива осуществляется по имени массива и индексу нужного элемента. Например, чтобы получить доступ к нулевому элементу вектора а (Рис. 18), нужно:
- ввести имя массива (а);
- нажать кнопку Subscript (Нижний индекс)  на панели Matrix (Матрица) либо ввести < [ > с клавиатуры;
на панели Matrix (Матрица) либо ввести < [ > с клавиатуры;
- в появившийся справа снизу от имени массива местозаполнитель нужно ввести желаемый индекс (0);
- ввести знак равенства (численного вывода).
Справа от знака равенства появится значение нулевого элемента вектора а, как показано во второй строке Рис. 18.
Чтобы получить доступ к элементу многоиндексного массива (например элементу а1,0 матрицы а из Рис.19), нужно:
- ввести имя массива (а);
- перейти к вводу нижнего индекса, нажав на клавиатуре < [ > ;
- ввести в местозаполнитель индекса первый индекс (1), запятую "," и в появившийся после запятой местозаполнитель введите второй индекс (0);
- нажать знак равенства.
В результате будет получен доступ к элементу, как показано в предпоследней строке Рис. 19.
Над элементами массива можно совершать действия как над обычными числами.
Создание массивов
Существует несколько способов создания массива:
1. ввод всех элементов вручную с помощью команды Insert / Matrix (Вставка / Матрица);
2. непосредственное присвоение отдельных элементов массива через оператор присваивания;
3. определение элементов массива с помощью ранжированной переменной и др.
Создание массива командой Insert / Matrix (Вставка / Матрица)
Самый простой и наглядный способ создания вектора или матрицы заключается в следующем:
- нужно задать имя массива (вектора или матрицы);
- ввести знак Присвоить : =(клавиша <:> двоеточие);
- нажать кнопку Matrix or Vector (Матрица или вектор) на панели Matrix (Матрица),

либо клавиши <Ctrl>+<M>, либо выбрать пункт меню Insert / Matrix (Вставка / Матрица);
- в диалоговом окне Insert Matrix (Вставка матрицы, Рис. 20) нужно задать целое число столбцов и строк матрицы, которую необходимо создать. Например, для создания вектора 3x1 нужно ввести показанные на Рис. 20 значения;
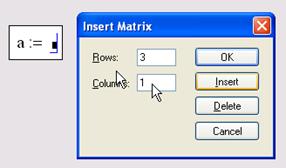
Рис. 20. Диалоговое окно «Вставка матрицы»
- нажать кнопку ОК или Insert (Вставить) — в результате в документ будет вставлена заготовка матрицы с определенным числом строк и столбцов (Рис.21);
- ввести значения элементов в местозаполнители матрицы. Переходить от одного элемента матрицы к другому можно с помощью указателя мыши, клавиши «табуляция», либо клавиш со стрелками.
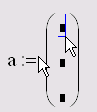
Рис. 21. Заполнение матрицы элементами Добавление в уже созданную матрицу строк или столбцов.
Добавление в уже созданную матрицу строк или столбцов производится точно так же:
- нужно выделить линиями ввода элемент матрицы, правее и ниже которого будет осуществлена вставка столбцов и (или) строк.
- вставить в него матрицу, как было описано выше. При этом число вставляемых столбцов или строк может быть равным нулю (Рис. 22).
- заполнить местозаполнители недостающих элементов матрицы.
На Рис. 22 и 23 показаны результаты последовательной вставки в матрицу столбца и строки через диалог Insert Matrix.

Рис. 22. Добавление одного столбца к матрице
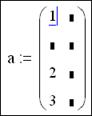
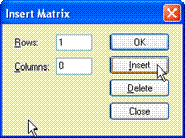
Рис. 23. Добавление одной строки к матрице
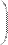
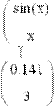
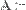 В местозаполнители элементов матрицы можно вставлять не только числа (действительные или комплексные), но и любые математические выражения, состоящие из переменных, операторов, встроенных и пользовательских функций (Рис. 24, вторая строка).
В местозаполнители элементов матрицы можно вставлять не только числа (действительные или комплексные), но и любые математические выражения, состоящие из переменных, операторов, встроенных и пользовательских функций (Рис. 24, вторая строка).

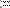
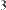
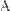
 Рис. 24. Использование переменных и функций при определении матрицы
Рис. 24. Использование переменных и функций при определении матрицы
Создание массива через непосредственное присвоение его элементов;
Массив можно определить, присваивая значения непосредственно отдельным его элементам
(Рис. 25);
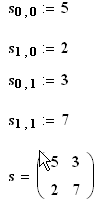
Рис. 25 Создание массива непосредственным присваиванием элементов.
Создание массива с помощью ранжированных переменных
Для присвоения значений элементам массива можно использовать ранжированные переменные
(Рис. 26).
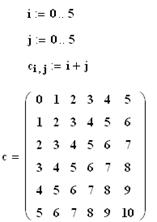
Рис. 26. Использование ранжированной переменной для определения матрицы
В любом месте документа допускается переопределение любого из элементов массива.
В местозаполнители элементов матрицы допускается вставка любых функций, подобно применению обычного оператора присваивания,
Отображение вывода векторов и матриц
Матрицы, векторы и ранжированные переменные отображаются по-разному в зависимости от того, как задан вывод массива (Рис. 27).
i := 0.. 7 xi=
xi:= 0.5 × i
|
ç ÷
ç 0.5 ÷
ç 1 ÷
ç ÷
x = ç
1.5
÷
ç 2 ÷
ç 2.5÷
ç 3 ÷
ç ÷
è 3.5 ø
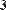
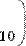

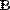
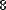 Рис. 26. Отображение массива в форме таблицы (слева) и матрицы (справа)
Рис. 26. Отображение массива в форме таблицы (слева) и матрицы (справа)
Простейшие операции с матрицами
Простейшие операции матричной алгебры реализованы в MathCAD в виде операторов. Векторы являются частным случаем матриц размерности Nх1, поэтому для них справедливы все те операции, что и для матриц, если ограничения особо не оговорены (например некоторые операции применимы только к квадратным матрицам NхN). Какие-то действия допустимы только для векторов (например скалярное произведение), а какие-то, несмотря на одинаковое написание, по-разному действуют на векторы и матрицы.
Непосредственное проведение векторных операций над матрицами-строками размерности 1хN, невозможно, нужно предварительно транспонировать строку для того чтобы превратить ее в вектор.
Транспонирование
Транспонированием называют операцию, при которой столбцы исходной матрицы становятся строками, а строки — столбцами. Чтобы транспонировать матрицу, нужно выделить ее и нажать кнопку Transpose (Транспонирование) на панели Matrix (Матрица) или нажать клавиши <Ctrl>+<1>.

Рис. 27. Кнопка Transpose (Транспонирование) на панели Matrix
Сложение и вычитание матриц

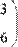
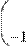
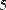
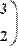

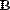
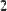 В MathCAD можно складывать матрицы и вычитать их друг из друга. Для этого применяются операторы <+> или <–>, соответственно. Матрицы должны иметь одинаковую размерность, иначе будет выдано сообщение об ошибке. Каждый элемент суммы двух матриц равен сумме соответствующих элементов матриц-слагаемых (Рис. 28).
В MathCAD можно складывать матрицы и вычитать их друг из друга. Для этого применяются операторы <+> или <–>, соответственно. Матрицы должны иметь одинаковую размерность, иначе будет выдано сообщение об ошибке. Каждый элемент суммы двух матриц равен сумме соответствующих элементов матриц-слагаемых (Рис. 28).
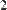
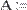
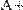

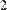
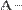

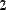
Рис. 28. Сложение и вычитание матриц
Сложение матрицы со скаляром
 MathCAD поддерживает операцию сложения матрицы со скаляром (Рис. 29). Каждый элемент результирующей матрицы равен сумме соответствующего элемента исходной матрицы и скалярной величины.
MathCAD поддерживает операцию сложения матрицы со скаляром (Рис. 29). Каждый элемент результирующей матрицы равен сумме соответствующего элемента исходной матрицы и скалярной величины.
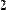
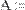
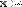
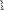
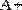
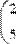
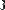
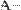





 Рис. 29 Сложение матрицы со скаляром
Рис. 29 Сложение матрицы со скаляром
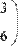
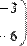
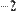

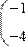

 Для того чтобы изменить знак матрицы, достаточно ввести перед ней знак минуса, как перед обычным числом (Рис. 30). Результат смены знака матрицы эквивалентен смене знака всех ее элементов.
Для того чтобы изменить знак матрицы, достаточно ввести перед ней знак минуса, как перед обычным числом (Рис. 30). Результат смены знака матрицы эквивалентен смене знака всех ее элементов.
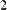
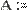
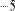
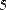 Рис. 30 Смена знака матрицы
Рис. 30 Смена знака матрицы
Умножение матриц
Матрицу размерности MхN допустимо умножать только на матрицу размерности NхP. В результате получается матрица размерности МхР.
Чтобы ввести символ умножения, нужно нажать клавишу со звездочкой <*> или воспользоваться панелью инструментов Matrix (Матрица), нажав на ней кнопку Dot Product (Умножение).

Рис. 31. Кнопка Умножение на панели Matrix
æ 1 3 ö
a := ç 1 6 ÷
ç ÷
è 5 0 ø
b :=æ 8 4 2 ö
è 8 9 3 ø
æ 32 a × b = ç 56
ç
è 40
31 11 ö
58 20 ÷
÷
20 10 ø
Рис. 32 Умножение матриц
Пример умножения матицы-строки на вектор и умножения вектора на матрицу-строку приведен на Рис. 33.
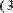
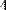
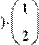

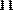
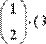
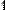
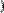

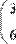
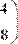
Рис. 33. Умножение вектора и строки
Рисунки 32 и 33 иллюстрируют тот факт, что при перемене мест сомножителей-матриц результат изменяется в отличии от перемножения скалярных чисел.
Умножение матрицы на скаляр

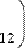
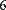

 Любую матрицу размерностью MхN можно умножать и делить на скаляр (Рис. 34).
Любую матрицу размерностью MхN можно умножать и делить на скаляр (Рис. 34).
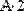
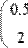
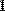
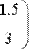


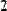
 Рис. 34. Умножение матрицы на скаляр
Рис. 34. Умножение матрицы на скаляр
Определитель квадратной матрицы
Определитель (Determinant) матрицы обозначается стандартным математическим символом. Чтобы ввести оператор нахождения определителя матрицы можно набрать на клавиатуре < | > (нажав клавиши <Shift>+<\>), или нажать кнопку Determinant (Определитель) на панели инструментов Matrix (Матрица) (Рис. 35).
Рис. 35. Кнопка Determinant (Определитель) на панели Matrix
В результате любого из этих действий появляется символ определителя с местозаполнителем 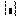 , в который следует поместить имя матрицы и нажать клавишу < = > (равно).
, в который следует поместить имя матрицы и нажать клавишу < = > (равно).
Результат вычисления определителя приведен на рис 36.
æ 36 31
D := ç 56 58
ç
è 40 20
11 ö
20 ÷
÷
10 ø

 D = 720
D = 720
Рис 36. Поиск определителя квадратной матрицы
Модуль вектора
Модуль вектора (vector magnitude) вычисляется так же, как и определитель матрицы. По определению, модуль вектора равен квадратному корню из суммы квадратов его элементов (Рис. 37).
æ 1 ö
a := ç 1 ÷
ç ÷
è 5 ø

 a = 5.196
a = 5.196
Рис. 37. Поиск модуля вектора
Сумма элементов вектора и след матрицы
Для вычисления суммы всех элементов вектора (только вектора) нужно нажать кнопку Vector Sum (Сумма элементов вектора) на панели Matrix (Матрица) (Рис. 38), или сочетание клавиш <Ctrl>+<4>.

Рис 38. Кнопка Vector Sum (Сумма элементов вектора) на панели Matrix (Матрица)
На экране появляется знак суммы с местозаполнителем 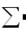 , в который вводится имя вектора.
, в который вводится имя вектора.
Результат выводится нажатием клавиши < = > (равно).
Сумму элементов матрицы по диагонали называют «следом матрицы» (trace). Вычисление следа матрицы организовано в виде встроенной функции tr( ):
tr(A) — след квадратной матрицы А.
æ 1 ö
a := ç 1 ÷
ç ÷
è 5 ø
æ 36
D := ç 56
ç
è 40
31 11 ö
58 20 ÷
÷
20 10 ø
åa = 7
tr(D) = 104
Рис. 39. Суммирование элементов вектора и диагонали матрицы
Обратная матрица
Поиск обратной матрицы возможен, если матрица квадратная, и ее определитель не равен нулю.
Для поиска обратной матрицы нужно нажать кнопку Inverse (Обратная матрица) на панели Matrix (Матрица) (Рис. 40), ввести в местозаполнитель 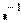 имя матрицы (Рис. 41) и нажать клавишу < = > (равно).
имя матрицы (Рис. 41) и нажать клавишу < = > (равно).

Рис 40. Кнопка Inverse (Обратная матрица) на панели Matrix (Матрица)
æ 36
D := ç 56
ç
è 40
31 11 ö
58 20 ÷
÷
20 10 ø
æ
D-1 = ç
ç
0.25
0.333
-0.125 -0.025 ö
-0.111 -0.144 ÷
÷
è -1.667
0.722
0.489 ø
Рис. 41 Поиск обратной матрицы
Произведение исходной матрицы на обратную матрицу представляет собой единичную матрицу, (у которой элементы главной диагонали равны 1, а все остальные элементы равны нулю).
Возведение матрицы в степень
К квадратным матрицам можно применять операцию возведения в целую степень. Результат данной операции приведен в Табл. 1. Ввести оператор возведения матрицы в степень можно точно так же, как и для скалярной величины: нажав кнопку Raise to Power (Возведение в степень) на панели
Calculator (Калькулятор)  или нажав клавишу < ^ >. После появления
или нажав клавишу < ^ >. После появления
местозаполнителя 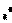 в него следует ввести имя матрицы и показатель степени и нажать клавишу < = > (равно).
в него следует ввести имя матрицы и показатель степени и нажать клавишу < = > (равно).
Таблица 1. Результаты возведения матрицы в степень
| n | Mn |
| единичная матрица размерности матрицы M | |
| сама матрица M | |
| -1 | M-1- матрица, обратная матрицеМ |
| M·M | |
| -2 | M-1· M-1 |
Дата добавления: 2014-12-24; просмотров: 2220;
