Вычисления.
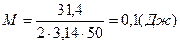 ,
, 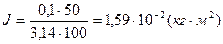 .
.
Ответ: 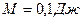 ,
, 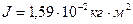 .
.
Задача 5. Платформа в виде диска радиусом 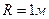 вращается по инерции с частотой
вращается по инерции с частотой 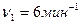 . На краю платформы стоит человек, масса которого
. На краю платформы стоит человек, масса которого 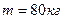 . С какой частотой
. С какой частотой 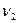 будет вращаться платформа, если человек перейдет в ее центр? Момент инерции платформы
будет вращаться платформа, если человек перейдет в ее центр? Момент инерции платформы 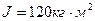 . Момент инерции человека рассчитывать как для материальной точки.
. Момент инерции человека рассчитывать как для материальной точки.
Дано:
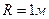 ;
;
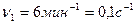 ;
;
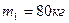 ;
;
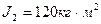
_________________
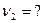
Решение.
Человек вместе с платформой составляет замкнутую механическую систему, поэтому момент импульса этой системы должен иметь постоянное значение.
Момент импульса системы в первом случае, когда человек стоял на краю платформы
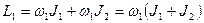 , (1)
, (1)
где 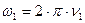 - угловая скорость вращения платформы и человека в первом случае,
- угловая скорость вращения платформы и человека в первом случае, 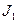 - момент инерции человека,
- момент инерции человека, 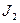 - момент инерции платформы.
- момент инерции платформы.
Момент инерции человека можно определить по формуле:
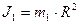 .
.
Когда человек перейдет в центр платформы, момент инерции человека станет равным нулю (расстояние до оси вращения 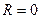 ), следовательно, во втором случае момент импульса человека станет равным нулю.
), следовательно, во втором случае момент импульса человека станет равным нулю.
Момент импульса системы во втором случае
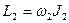 ,
,
где 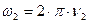 - угловая скорость вращения платформы во втором случае.
- угловая скорость вращения платформы во втором случае.
Запишем закон сохранения импульса:
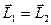 ;
;
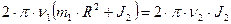 ;
;
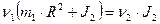 ;
;
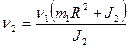 ;
;
Производим проверку размерности расчетной формулы:
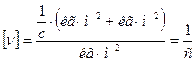 .
.
Вычисление:
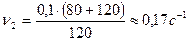 .
.
Ответ: если человек перейдет в центр платформы, платформа будет вращаться с частотой равной 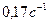 .
.
Задача 6. Два точечных заряда 6,7 нКл и (- 13,2)нКл находятся на расстоянии 5 см друг от друга. Найти напряженность электрического поля в точке, расположенной на расстоянии 3см от положительного заряда и 4см от отрицательного.
 Дано: Решение
Дано: Решение
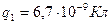
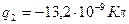
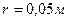
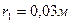
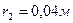
______________
Е - ? Электрическое поле создается двумя зарядами, поэтому
напряженность в данной точке поля находим по принципу
суперпозиции для напряженности.
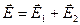 (1).
(1).
Поскольку заряды 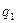 и
и 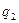 точечные, то по определению их напряженности вычисляются по формулам
точечные, то по определению их напряженности вычисляются по формулам 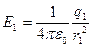 ,
, 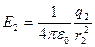 (2).
(2).
Из условия задачи следует, что угол между векторами 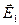 и
и 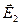 прямой. Тогда результирующую напряженность можно найти по теореме Пифагора
прямой. Тогда результирующую напряженность можно найти по теореме Пифагора
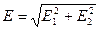 (3). Подставляем формулы (2) в (3)
(3). Подставляем формулы (2) в (3)
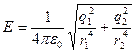 .
.
Проверка размерности 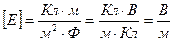 .
.
Дата добавления: 2014-12-04; просмотров: 1114;
