Ответ: , , .
Задача 3. Автомобиль движется вверх по наклонной плоскости с начальной скоростью 20 м/с. Определить путь, пройденный автомобилем до остановки и время его движения, если коэффициент трения 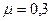 , а угол наклона
, а угол наклона  .
.
 Дано Решение
Дано Решение
| |
| |

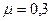

_____________
S - ?, t -?
Автомобиль движется вверх и останавливается, т.е. движение равнозамедленное. Конечная скорость равна нулю  . Ось Х направлена вдоль наклонной плоскости вверх, ось У – перпендикулярно наклонной плоскости.
. Ось Х направлена вдоль наклонной плоскости вверх, ось У – перпендикулярно наклонной плоскости.
При равнозамедленном движении 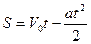 ,
, 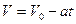 , т.к.
, т.к.  , следовательно
, следовательно 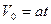 , откуда выразим время t:
, откуда выразим время t: 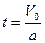 .
.
Подставим данное выражение в формулу для пройденного пути, находим 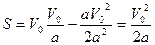 .
.
Вычисляем ускорение 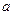 , с которым движется автомобиль, используя второй закон Ньютона.
, с которым движется автомобиль, используя второй закон Ньютона.
На автомобиль действуют три силы: сила тяжести 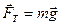 , сила реакции опоры
, сила реакции опоры  и сила трения
и сила трения 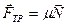 .
.
Записываем второй закон Ньютона в векторной форме 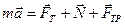 .
.
Проецируем это уравнение на оси ОХ и ОУ:
ОХ: 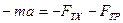 ,
,
ОУ: 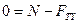 , откуда
, откуда 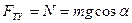 , тогда
, тогда 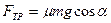 .
.
Проекция силы тяжести на ось ОХ равна 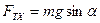 .
.
Получаем 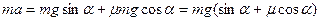 , откуда
, откуда 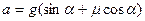
Подставляем найденное выражение для ускорения в выражения для определения искомых величин :
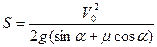 ,
,  .
.
Проверяем размерность
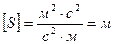 .
. 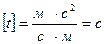 .
.
Вычисления
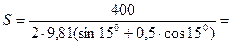

Ответ:
Задача 4. Вентилятор вращается с частотой 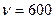 об/мин. После выключения он начал вращаться равнозамедленно и, сделав N=50 оборотов, остановился. Работа А сил торможения равна 31,4 Дж. Определить момент сил торможения М и момент инерции J вентилятора.
об/мин. После выключения он начал вращаться равнозамедленно и, сделав N=50 оборотов, остановился. Работа А сил торможения равна 31,4 Дж. Определить момент сил торможения М и момент инерции J вентилятора.
 Дано Решение
Дано Решение
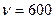 об/мин = По определению работа
об/мин = По определению работа 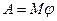 (1), где М – момент
(1), где М – момент
= 10 об/с тормозящей силы, 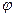 - угол поворота.
- угол поворота.
N=50 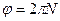 . Из (1) выражаем М :
. Из (1) выражаем М :  .
.
А = 31,4 Дж Для нахождения момента инерции записываем основное
______________ уравнение вращательного движения 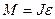 , откуда
, откуда
М-? J- ?  (2) , где
(2) , где 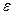 - угловое ускорение. Найдем
- угловое ускорение. Найдем 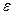 ,
,
используя то, что вентилятор вращается
равнозамедленно.
При равнозамедленном вращении 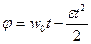 ,
, 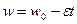 .
.
Так как вентилятор останавливается  , следовательно
, следовательно 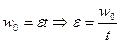 . По определению
. По определению 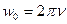 .
.  , откуда находим время вращения вентилятора до полной остановки
, откуда находим время вращения вентилятора до полной остановки 
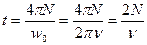 ,
,
 , подставляя это выражение в (2), получаем
, подставляя это выражение в (2), получаем 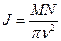 .
.
Проверка размерности 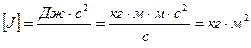
Дата добавления: 2014-12-04; просмотров: 3455;
