Дифференциальные уравнения второго порядка
Дифференциальное уравнение второго порядка (Д.У. — II) содержит вторую производную некоторой функции, саму эту функцию, независимую переменную и первую производную
Д.У.-II можно записать в виде:
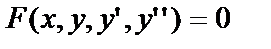 или
или
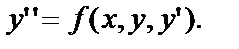
Определение. Общим решением Д.У. – II называется функция 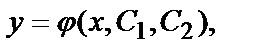 зависящая от двух произвольных постоянных
зависящая от двух произвольных постоянных 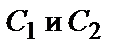 такая, что
такая, что
1) она удовлетворяет уравнению при любых значениях постоянных 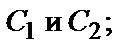
2) каковы бы ни были начальные условия 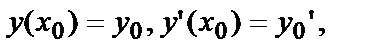 можно найти такие значения
можно найти такие значения 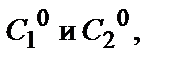 при которых функция
при которых функция 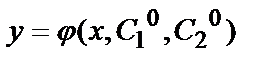 удовлетворяет этим условиям.
удовлетворяет этим условиям.
Всякая функция, полученная из общего решения при конкретных значениях постоянных 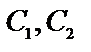 называется частным решением Д.У. – II.
называется частным решением Д.У. – II.
Заметим, что начальные условия для Д.У. – II представляют собой заданные значения функции 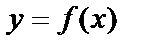 и её производной
и её производной 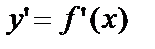 при одном и том же данном значении независимой переменной х0. Их обычно записывают:
при одном и том же данном значении независимой переменной х0. Их обычно записывают: 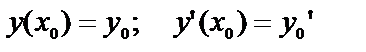 или
или 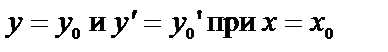 или
или 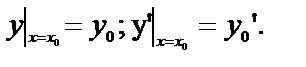 Т.е. задать начальные условия для Д.У. – II значит задать три числа:
Т.е. задать начальные условия для Д.У. – II значит задать три числа: 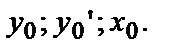
Например, для Д.У. – II
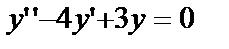 общее решение
общее решение 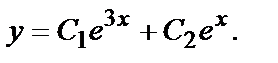
Убедимся в этом проверкой. Если 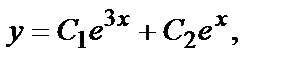 то
то 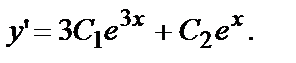
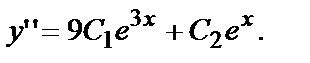
Подставив 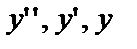 в данное уравнение, получим
в данное уравнение, получим
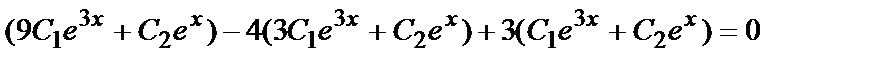 — верное равенство.
— верное равенство.
Найдём частное решение этого уравнения, удовлетворяющее начальным условиям: 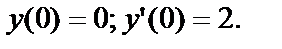 Подставим в
Подставим в 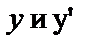 эти условия:
эти условия:
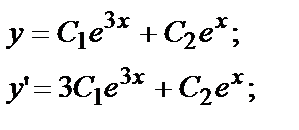
| { | 0= 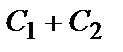 2=3
2=3 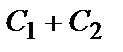
|
Решив эту систему, получим значения для постоянных 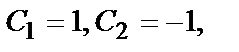 при которых из общего решения
при которых из общего решения 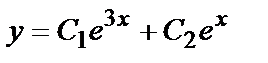 выделим искомое частное решение:
выделим искомое частное решение:

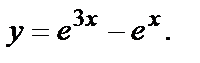
Рассмотрим некоторые виды дифференциальных уравнений второго порядка и способы их решения.
Дата добавления: 2014-12-30; просмотров: 1269;
