Линейные дифференциальные уравнения второго порядка

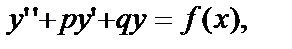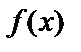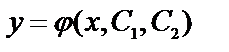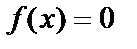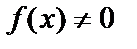Уравнение вида где p и q – данные постоянные коэффициенты, - любая дифференцируемая функция от х, будем называть линейным дифференциальным уравнением второго порядка с постоянными коэффициентами. Его общее решение зависит от двух произвольных постоянных. При уравнение называется линейным однородным Д.У. – II с постоянными коэффициентами. При уравнение 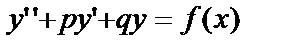называется линейным неоднородным Д.У. – II с постоянными коэффициентами. Рассмотрим способ решения однородного Д.У. – II с постоянными коэффициентами 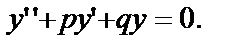Общее решение уравнения находится с помощью характеристического уравнения: 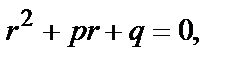которое получится, если, сохранив в данном Д.У. – II коэффициенты 1, p, q, заменить функцию y единицей, а производные соответствующими степенями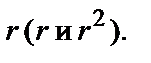

Так, для уравнения характеристическим будет уравнение 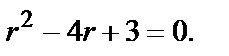Для уравнения 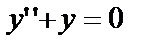характеристическим будет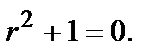

Для всякого линейного Д.У. – II с постоянными коэффициентами характеристическим является алгебраическое уравнение второй степени (квадратное уравнение).