Дифференциальные уравнения второго порядка, допускающие понижение порядка
Из этого заголовка видно, что речь пойдёт о Д.У. – II, решение которых сводится к решению дифференциальных уравнений первого порядка. Простейшими из таких уравнений являются уравнения вида 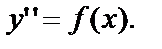 Д.У.-II содержит только вторую производную и некоторую функцию от х (ни сама функция у, ни её производная
Д.У.-II содержит только вторую производную и некоторую функцию от х (ни сама функция у, ни её производная 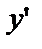 в уравнение не входят).
в уравнение не входят).
Уравнение вида 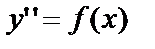 решается последовательно интегрированием два раза.
решается последовательно интегрированием два раза.
№ 12.Например: 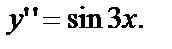
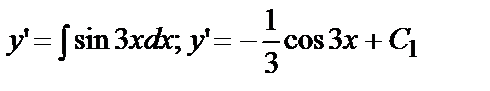 - это уравнение уже первого порядка.
- это уравнение уже первого порядка.
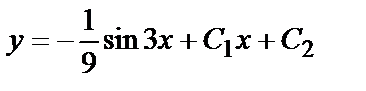 - общее решение исходного уравнения (содержит две постоянные
- общее решение исходного уравнения (содержит две постоянные 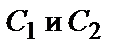 ).
).
Заметим, что аналогично решаются и дифференциальные уравнения порядка выше второго, если они имеют вид, например 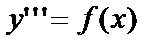 или
или 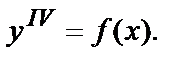
Рассмотрим уравнения:
№ 13. 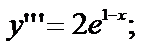
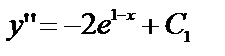
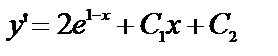
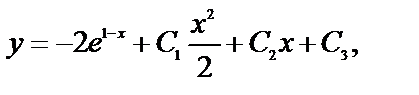
№ 14. 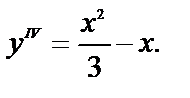
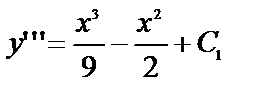
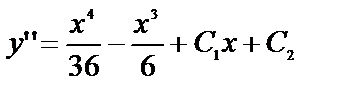
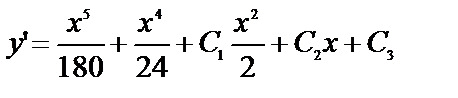
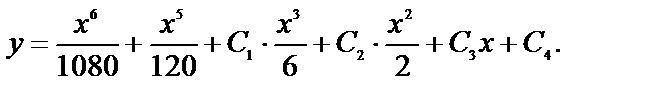
Обратите внимание, общее решение дифференциального уравнения третьего порядка содержит три произвольные постоянные, а дифференциальное уравнение четвёртого порядка – уже четыре.
Допускают понижение порядка и дифференциальные уравнения вида 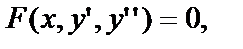 т.е. уравнения, в которые не входит сама искомая функция у.
т.е. уравнения, в которые не входит сама искомая функция у.
Решается уравнение вида
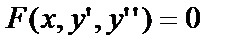
подстановкой 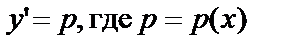 - вспомогательная функция. Тогда
- вспомогательная функция. Тогда 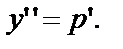 Поставив
Поставив 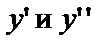 в данное уравнение Д.У. – II, получим
в данное уравнение Д.У. – II, получим 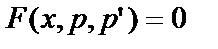 - уравнение первого порядка.
- уравнение первого порядка.
Рассмотрим
№ 15. Найти частное решение уравнения
(1) 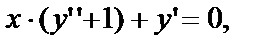 удовлетворяющее начальным условиям
удовлетворяющее начальным условиям 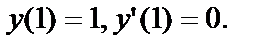
Подставновка 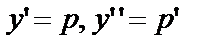 приводит к уравнению первого порядка
приводит к уравнению первого порядка 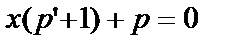 (2) относительно функции p и её производной
(2) относительно функции p и её производной 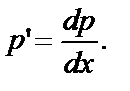 Переменные p и x в нём разделить нельзя, поэтому проверим его на однородность, подставив в (2)
Переменные p и x в нём разделить нельзя, поэтому проверим его на однородность, подставив в (2) 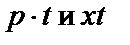 вместо p и x соответственно. Видно, что (2) — однородное Д.У. – I. Решаем его подстановкой
вместо p и x соответственно. Видно, что (2) — однородное Д.У. – I. Решаем его подстановкой 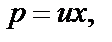
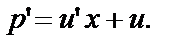
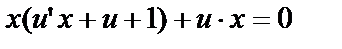 или
или
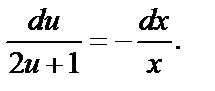
Интегрируя, получим: 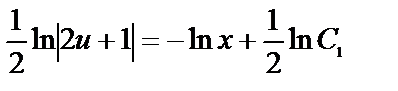 или
или 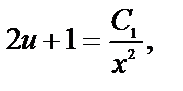 т.к.
т.к. 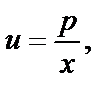 то
то 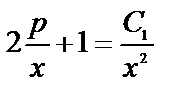 или
или 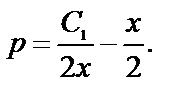
Исходное уравнение (1) решалось подставновкой 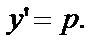 Поэтому
Поэтому 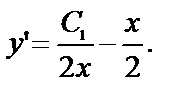 Интегрируя, получим
Интегрируя, получим 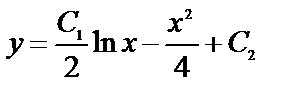 - общее решение (1).Учитывая данные начальные условия
- общее решение (1).Учитывая данные начальные условия 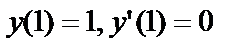 , получим
, получим
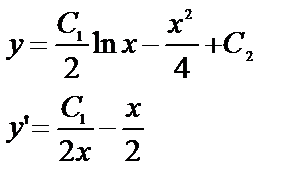
| 
|
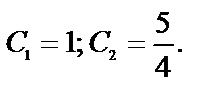 Подставив найденные
Подставив найденные 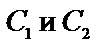 в общее решение, получим
в общее решение, получим 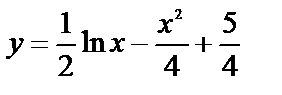 — частное решение данного уравнения (1).
— частное решение данного уравнения (1).
Проверка. Если  то
то
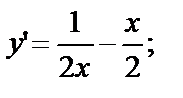
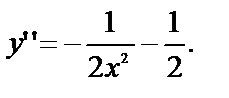
Подставим 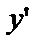 и
и 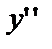 в уравнение
в уравнение 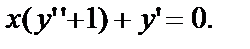
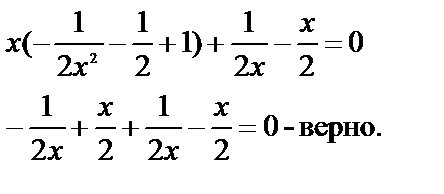
Дата добавления: 2014-12-30; просмотров: 1297;
