Вероятностная оценка случайной величины – наработки до второго отказа.
| Определяемая величина | Номера интервалов наработки до второго отказа | ||||||||
| Границы интервала наработки | ∆L | 26-28 | 28-30 | 30-32 | 32-34 | 34-36 | 36-38 | 38-40 | 40-42 |
| Значение середины интервала | Li | ||||||||
| Число вторых отказов в интервале | ni | ||||||||
| Число вторых отказов к наработке Li | m(L) | ||||||||
| Оценка Вероятности второго отказа | F2(L) | 0,04 | 0,1 | 0,18 | 0,22 | 0,4 | 0,64 | 0,94 | 1,00 |
| Плотность вероятности второго отказа | f2(L) | 0,02 | 0,03 | 0,04 | 0,02 | 0,09 | 0,12 | 0,15 | 0,03 |
| Вероятность | wi | 0,04 | 0,06 | 0,08 | 0,04 | 0,18 | 0,24 | 0,3 | 0,06 |
Закономерности изменения потока отказов описывают изменение по наработке показателей, характеризующих процесс возникновения и устранения отказов автомобилей.
Очевидно, что наработки на отказы, во-первых, случайны для каждого автомобиля и описываются соответствующей функцией f(L), во-вторых, эти наработки независимы для разных автомобилей, в третьих, при устранении отказа в зоне ремонта безразлично, какой автомобиль отказал или какой отказ по счету.
К важнейшим характеристикам этих закономерностей относятся средняя наработка до k-го отказа Lk, средняя наработка между отказами для n изделий Lk,k+1, коэффициент полноты восстановления ресурса h, ведущая функция потока отказов W(L) и параметр потока отказов w(L).
Средняя наработка до k-го отказа:
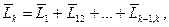(14)
где L1 - средняя наработка до первого отказа;
L12 - средняя наработка между первым и вторым отказом
Lk=39,634+19,874=59,508
Средняя наработка между (k-1)-м и k-м отказами для n автомобилей:
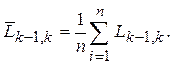(15)
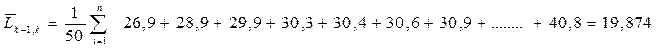
Коэффициент полноты восстановления ресурса характеризует возможность сокращения ресурса после ремонта:
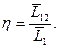
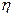=19,874/39,634=0,5 (16)
Сокращение ресурса после первого и последующего ремонтов, которое необходимо учитывать при планировании и организации работ по обеспечению работоспособности объясняется: частичной заменой только отказавших деталей, при значительном сокращении надежности других, особенно сопряженных; использованием в ряде случаев запасных частей и материалов худшего качества, чем при изготовлении автомобиля; низким технологическим уровнем работ.
Ведущая функция потока отказов (функция восстановления) определяет накопленное количество первых и последующих отказов изделия к наработке L. В курсовой работе определяем данную функцию для трех любых точек на оси наработки L (рис.6), лежащих в интервале от средней наработки до первого отказа, до средней наработки до второго отказа.Как
следует из рисунков 4 и 5, из-за вариации наработок на отказы происходит смешение отказов, а функции вероятностей 1-го и 2-го отказов F1(L) и F2(L)частично накладываются друг на друга.
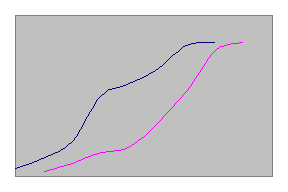
Рис. 6.Формирование ведущей функции восстановления
В общем виде ведущая функция потока отказов:
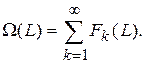(17)
W(L1)=0,04
W(L2)= 0,1
W(L3)=0,18
W(L4)=0,22
W(L5)=0,4
W(L6)=0,64
W(L7)=0,94
W(L8)=1,00
Для каждого частного случая:
L1: W(L1)= F1(L1) произошел только 1-й отказ.
L2: W(L2)=F1(L2)+ F2(L2) произошел 1-й и 2-й отказ.
L3: W(L3)=F1(L3)+ F2(L3) произошел 1-й и 2-й отказ.
Процесс формирования ведущей функции восстановления представлен на рис.6.
Для практического расчета W(L) необходимо вычислить вероятности первого, второго и т.д. отказов и просуммировать их.
Параметр потока отказов w(L) - это плотность вероятности возникновения отказов восстанавливаемого изделия, определяемая для данного момента времени или пробега:
w(L)=dΩ(L)/dL или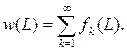 
(18)
w(L)=0,02
w(L)=0,03
w(L)=0,04
w(L)=0,02
w(L)=0,09
w(L)=0,12
w(L)=0,15
w(L)=0,03
Иными словами w(L) – это относительное число отказов, приходящееся на единицу пробега или времени работы одного изделия. Следует отметить, что ведущая функция и параметр потока отказов определяется аналитически как функции параметров этих законов лишь для некоторых видов законов распределения. Наиболее часто встречаются нормальный, логарифмически нормальный, Вейбулла-Гнеденко и экспоненциальный законы.
Например, для экспоненциального закона:
.
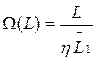Откуда следует, что:
.
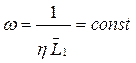Для нормального закона:
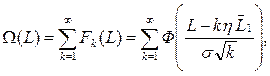(19)
где Ф - нормированная функция для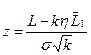 
;
k - число отказов.
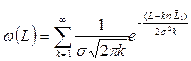. (20)
В рассматриваемом нами примере курсовой работы средняя наработка до первой замены изделия равна 40 тыс. км, среднее квадратическое отклонение равно 20 тыс. км, а коэффициент полноты восстановления ресурса составляет 0,54. Необходимо определить возможное число замен при произвольно взятом пробеге в интервале между средними наработками до первого и второго отказа автомобиля. В интервале от 52 до 68 тыс. км, произвольно выберем пробег равный 60 тыс.км.
Для расчетов используем формулу (19) последовательно определяя F1, F2, F3 и т. д.
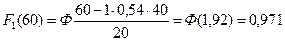
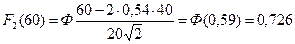
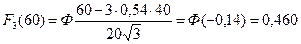
Ввиду того, что F3 мало, последующие расчеты для F4 и других можно не производить. Таким образом, к пробегу 60 тыс. км возможное число замен данной детали составит:
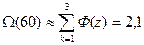
Для практического использования важны некоторые приближенные оценки ведущей функции параметра потока отказов
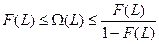(20)
Из этой формулы следует, что на начальном участке работы, где преобладают первые отказы, т.е. F(L) ≤ 1, W(L)» F(t).
Ведущая функция параметра потока отказов стареющих элементов для любого момента времени удовлетворяет следующему неравенству:
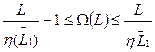(21)
Для рассмотренного выше примера, используя формулу (21) получим следующую оценку ведущей функции параметра потока отказов при пробеге автомобиля L=60 тыс. км; 1,0£W(L)£2,1. Таким образом, к пробегу L в среднем (формула (20)) возможно от 1,0 до 2,1 отказов изделия, по точным расчетам (формула (19)) эта величина составляет 2,1 отказов.
На этом заканчивается раздел посвященный рассмотрению практического использования теории надежности техники.
Дата добавления: 2014-12-08; просмотров: 1756;