Вернёмся к решению однородного линейного Д.У. – II с постоянными коэффициентами

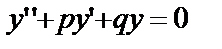(1)

и характеристическим уравнением

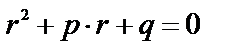(2)

Возможны три случая:

1) если корни характеристического уравнения (2) действительны и различны 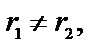то общее решение Д.У. – II (1)

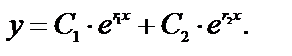
2) если корни уравнения (2) действительны и одинаковы 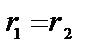(обозначим их 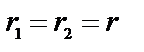), то общее решение уравнения (1)

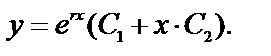
3) если корни уравнения (2) 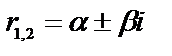представляют собой пару взаимно–сопряжённых комплексных чисел с действительной частью 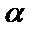и с коэффициентом мнимой части 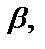то общее решения уравнения (1)

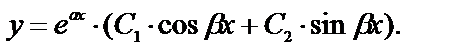
Рассмотрим примеры:

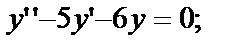
1) 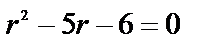— характ. уравнение

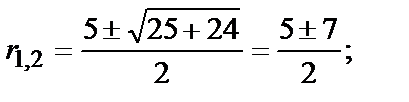
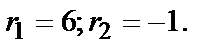
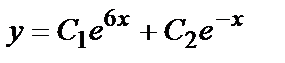- общее решение.

2)

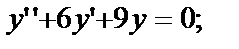
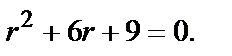
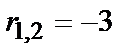— два равных корня.

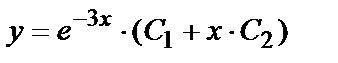- общее решение.

3)

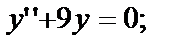
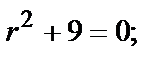
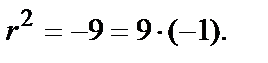
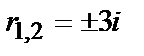— комплексные корни ( ).

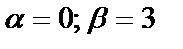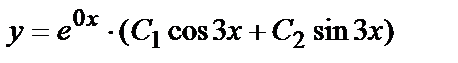или 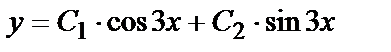— общее решение.

4) Найти частное решение уравнения 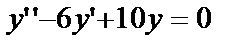при 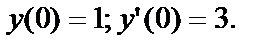Составим и решим характеристич. уравнение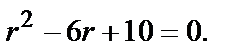

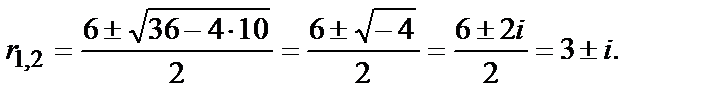
Общее решение 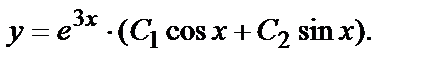Найдём производную

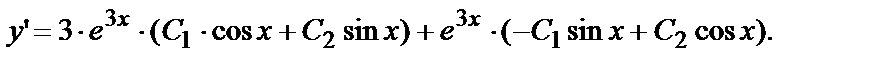
Подставив начальные условия, получим систему для определения.

С₁ и С₂:

{

{

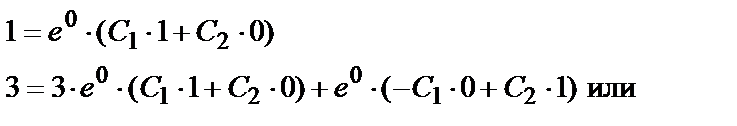
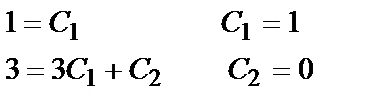
Подставив полученные значения в общее решение, получим 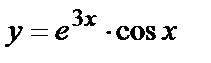- искомое частное решение.

Проверка. Найдём для функции 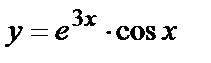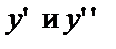и подставим в данное уравнение.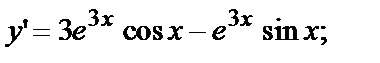

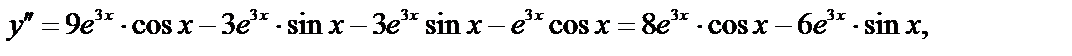
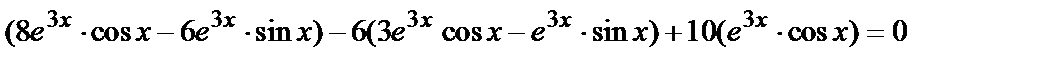— верное равенство, т.е. частное решение найдено верно.