Дифференциальные уравнения второго порядка. Линейные однородные уравнения второго порядка с постоянными коэффициентами

Линейные однородные уравнения второго порядка с постоянными коэффициентами

Общий вид такого уравнения: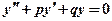

где p и q -действительные числа. Корни его характеристического уравнения 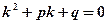могут быть:

1) действительными и различными: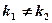

2) действительными и равными: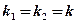

3) комплексными: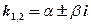

Им соответствуют следующие общие решения уравнения:

1) ;

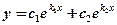2) ;

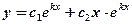3) .

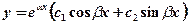Пример 3.

Найти частное решение линейного однородного уравнения второго порядка с постоянными коэффициентами, удовлетворяющее начальным условиям:

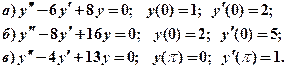
Решение:

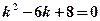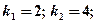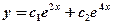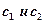а) Характеристическое уравнение имеет два различных вещественных корня , поэтому общее решение этого дифференциального уравнения записывается в виде , где произвольные постоянные.

Отсюда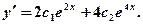

Основываясь на начальных условиях, получаем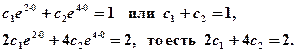

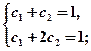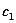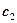Решая систему уравнений получаем =1; =0.

Частное решение данного уравнения, удовлетворяющего заданным начальным условиям, приобретает вид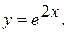

б) Характеристическое уравнение 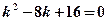имеет два равных корня 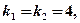поэтому общее решение соответствующего дифференциального уравнения будет иметь вид 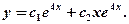Дифференцируя, получим .

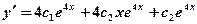Учитывая начальные условия, получаем систему для определения 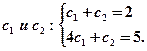Откуда 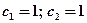, поэтому частное решение имеет вид: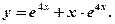

в) Характеристическое уравнение 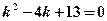не имеет действительных корней. Его корни: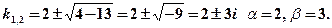

Поэтому общее решение данного уравнения имеет вид: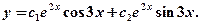

Дифференцируя, получим:

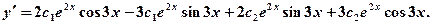
Подставляя в выражения для 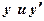начальные условия, получим систему уравнений: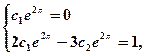

решая которую, найдем .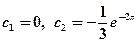

Тогда частное решение данного уравнения будет иметь вид: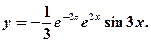

Линейные неоднородные уравнения второго порядка с постоянными коэффициентами

Общий вид такого уравнения: (*)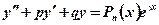

В правой части: 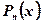многочлен степени .

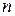Общее решение уравнения (*)может быть представлено в виде

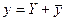
где 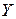- общее решение соответствующего линейного однородного уравнения,

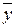- какое- либо частное решение неоднородного уравнения (*).

Для отыскания 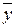пользуются следующим правилом:

1) если число 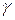не является корнем характеристического уравнения, то 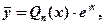где 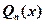- многочлен степени с неопределенными коэффициентами;

2) если число 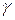совпадает с одним из корней характеристического уравнения, то

;

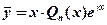3) если число 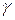совпадает с обоими корнями характеристического уравнения , то

.

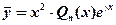Пример 4

Найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами: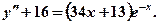

Решение:

Будем искать общее решение в виде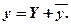

Y – общее решение уравнения 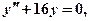характеристическое уравнение которого 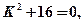а его корни 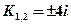и решение Y имеет вид:

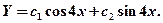
Частное решение 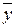будем искать в виде

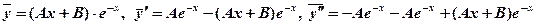или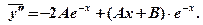

Подставим 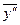и 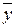в исходное уравнение, получим:

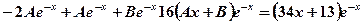или

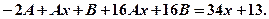
Составим систему для нахождения А и В.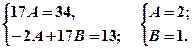

Тогда частное решение имеет вид: .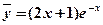

Общее решение данного уравнения будет:

.

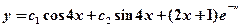Варианты индивидуальных заданий