Дифференциальные уравнения первого порядка. Уравнение с разделенными переменными

Уравнение с разделенными переменными

Общий вид:

Его общий интеграл: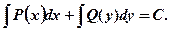

Уравнение с разделяющимися переменными

Его общий вид: 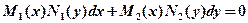или .

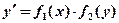Разделяя переменные: 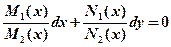, получаем дифференциальное уравнение с разделенными переменными.

Однородное дифференциальное уравнение первого порядка

Это уравнение вида: 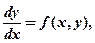если функция 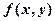удовлетворяет условию 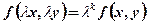, k=const

Уравнение первого порядка 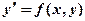называется однородным, если 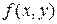можно представить как функцию только одного отношения переменных 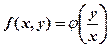, т.е. уравнения вида .

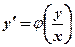Однородное уравнение приводится к уравнению с разделяющимися переменными подстановкой у=ux (или x=uy), где u=u(x) ( u=u(y) )- новая функция.

Пример 1.

Найти общий интеграл данного уравнения:

Решение:

Это однородное уравнение, т.к.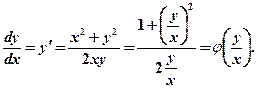

Далее вводим новую функцию 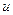, полагая 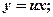при этом 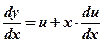и после подстановки данное уравнение преобразуется в уравнение с разделяющимися переменным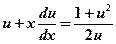и или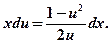

Разделим переменные: 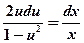и, интегрируя, найдем 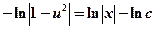или 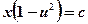. Исключая вспомогательную функцию 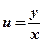, окончательно получим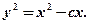

Линейные уравнения первого порядка

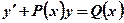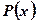Это уравнения вида: , где и 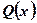- известные функции от х.

Посредством замены функции произведением двух вспомогательных функций 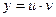линейное уравнение сводится к двум уравнениям с разделяющимися переменными относительно каждой из вспомогательных функций.

Пример 2

Решить уравнение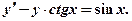

Решение:

Убедившись, что данное уравнение линейное, полагаем 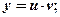тогда 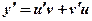и данное уравнение преобразуется к виду:

Так как одну из вспомогательных функци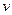й или 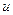можно взять произвольно, то выберем в качестве 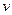какой – либо частный интеграл уравнения 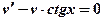(1)

Тогда для отыскания 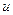получим уравнение: 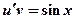(2)

Решая первое уравнение, найдем 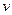. Разделяя переменные и интегрируя, найдем его простейший, отличный от нуля частный интеграл:

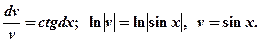
Подставляя v во второе уравнение и решая его, найдем 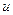как общий интеграл этого уравнения: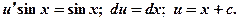

Зная 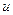и 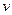, находим искомую функцию .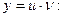

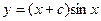Уравнение Бернулли

Его общий вид: 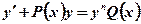. Данное уравнение отличается от линейного тем, что в правую часть входит множителем некоторая степень функции . Решается оно так же, как и линейное. Посредством подстановки 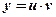сводится к двум уравнениям с разделяющимися переменными.