Дифференциальные уравнения II порядка.
Определение.Уравнение, связывающее независимую переменную, неизвестную функцию, ее первую производную, а тек же вторую производную от искомой функции, называется дифференциальным уравнением второго порядка.
В общем случае дифференциальное уравнение второго порядка можно записать в виде F (х, у, у',y") = 0, где у= у(х)-искомая функция.
Одним из представителей дифференциальных уравнений второго порядка является линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Уравнение вида 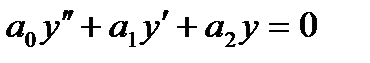 (1), где
(1), где 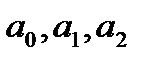 - действительные числа
- действительные числа 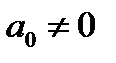 , называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Чтобы решить уравнение (1), нужно решить характеристическое уравнение
, называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Чтобы решить уравнение (1), нужно решить характеристическое уравнение 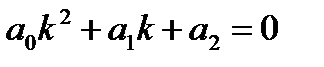 (2)
(2)
При решении характеристического уравнения (2) возможны три случая, в зависимости от которых строится общее решение данного дифференциального уравнения (1):
| Корни уравнения(2) | Частные решения уравнения (1) | Общее решение уравнения (1) |
Действительные и различные: 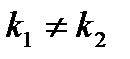
| 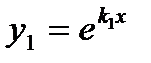
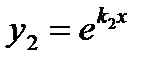
| 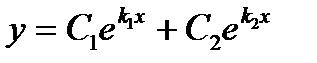
|
Равные: 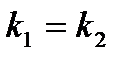
| 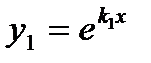
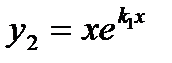
| 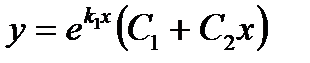
|
Комплексно-сопряженные: 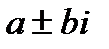
| 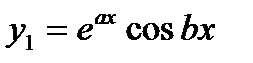 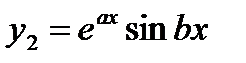
| 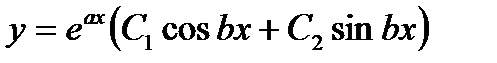
|
Пример 1.Найти общее решение дифференциального уравнения 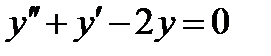
Решение. Характеристическое уравнение имеет вид 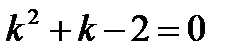 . Его корни
. Его корни 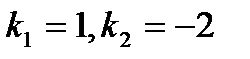 . Так как корни действительные и различные, то общее решение записывается в виде
. Так как корни действительные и различные, то общее решение записывается в виде 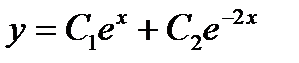 .
.
Пример 2. Найти общее решение дифференциального уравнения 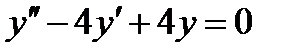
Решение. Характеристическое уравнение 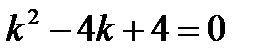 имеет равные корни
имеет равные корни 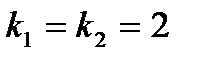 . Следовательно, общее решение данного уравнения таково:
. Следовательно, общее решение данного уравнения таково: 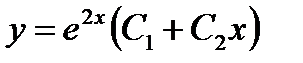 .
.
Пример 3. Найти общее решение дифференциального уравнения 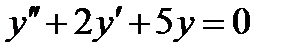
Решение. Характеристическое уравнение 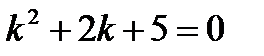 имеет комплексно-сопряженные корни:
имеет комплексно-сопряженные корни: 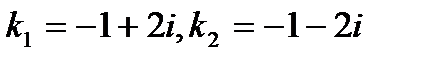 . Таким образом, общее решение уравнения записывается в виде
. Таким образом, общее решение уравнения записывается в виде 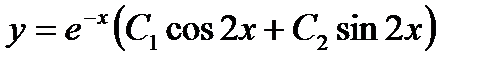
Пример 4. Найти частное решение уравнения 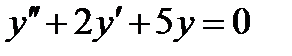 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 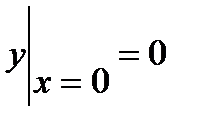 ,
, 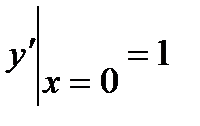
Решение. Общее решение уравнения записывается в виде
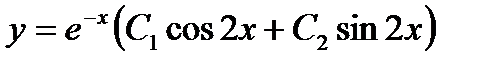
Найдем частное решение, которое удовлетворяет заданным начальным условиям. Из первого условия следует, что 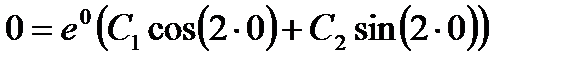 ,
, 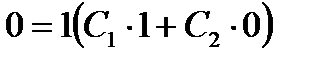 , откуда
, откуда 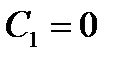 . Учитывая, что
. Учитывая, что 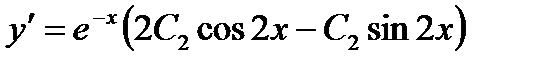 , и используя второе начальное условие, находим
, и используя второе начальное условие, находим 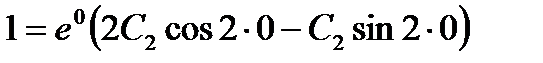 ,
, 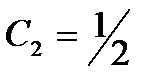 . Следовательно, искомое частное решение имеет вид
. Следовательно, искомое частное решение имеет вид 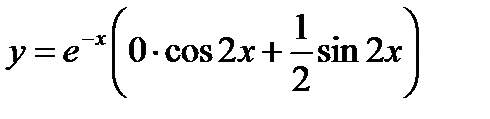 ,
, 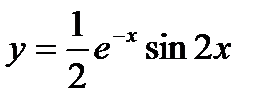
Пример 5. Найти интегральную кривую дифференциального уравнения 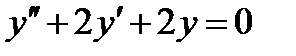 , проходящую через точку
, проходящую через точку 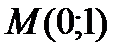 и касающуюся в этой точке прямой
и касающуюся в этой точке прямой 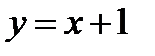 .
.
Решение. Характеристическое уравнение имеет вид 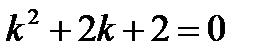 ; его корни
; его корни 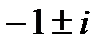 являются комплексно-сопряженными. Уравнение множества интегральных кривых запишется так
являются комплексно-сопряженными. Уравнение множества интегральных кривых запишется так 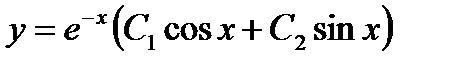 :
:
Найдем уравнение искомой интегральной кривой, для чего в равенства
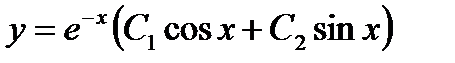 и
и 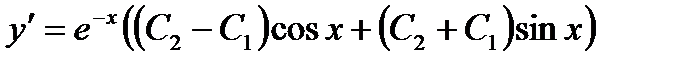 подставим значения у = 1 и углового коэффициента касательной
подставим значения у = 1 и углового коэффициента касательной 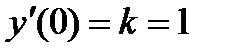 . В результате получим
. В результате получим 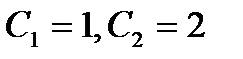 . Подставив эти значения в общее решение, получим
. Подставив эти значения в общее решение, получим 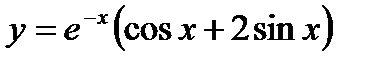 .
.
Содержание работы.
Задание 1. Найдите общее решение дифференциального уравнения первого порядка с разделяющимися переменными:
1.1 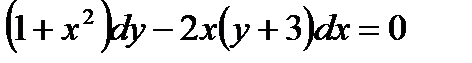
1.2 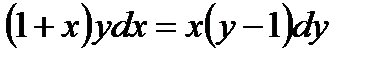
1.3 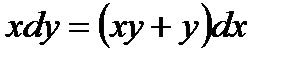
1.4 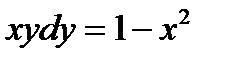
1.5 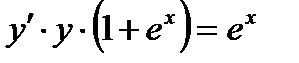
Задание 2. Найдите общее решение однородного дифференциального уравнения первого порядка:
2.1 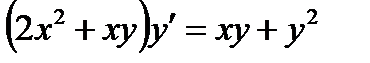
2.2 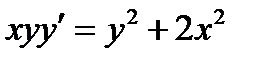
2.3 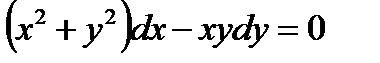
2.4 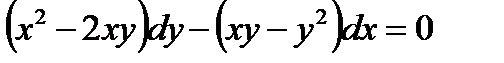
2.5 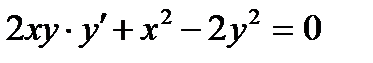
Задание 3. Найдите общее и частное решения линейного дифференциального уравнения первого порядка:
3.1 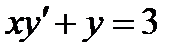 , если
, если 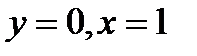
3.2 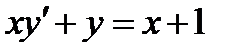 , если
, если 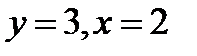
3.3 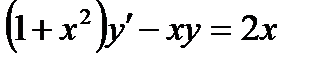 , если
, если 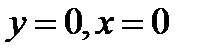
3.4 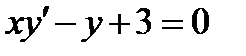 , если
, если 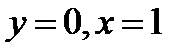
3.5 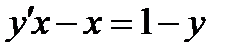 , если
, если 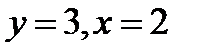
Задание 4. Найдите общее решение линейного однородного дифференциального уравнение второго порядка с постоянными коэффициентами:
4.1 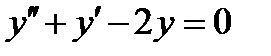
4.2 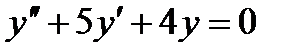
4.3 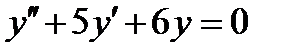
4.4 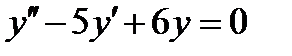
4.5 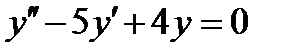
Задание 5. Найдите общее и частное решения линейного однородного дифференциального уравнение второго порядка с постоянными коэффициентами:
5.1 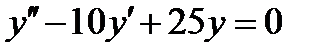 , если
, если 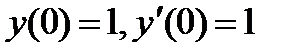
5.2 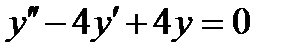 , если
, если 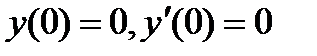
5.3 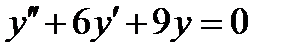 , если
, если 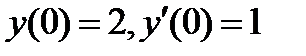
5.4 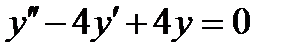 , если
, если 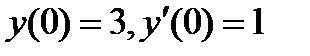
5.5 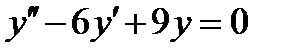 , если
, если 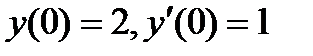
Задание 6. Найдите общее и частное решения линейного однородного дифференциального уравнение второго порядка с постоянными коэффициентами:
6.1 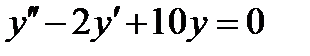 , если
, если 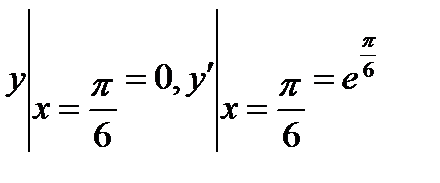
6.2 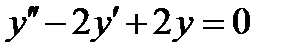 , если
, если 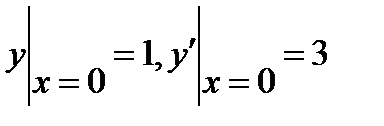
6.3 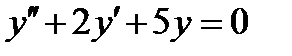 , если
, если 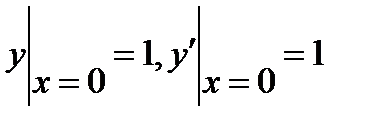
6.4 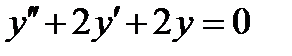 , если
, если 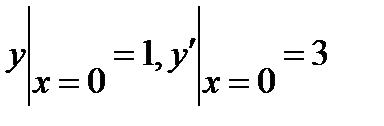
6.5 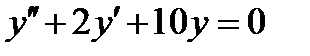 , если
, если 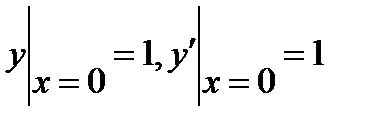
Вопросы для самоконтроля
- Какое уравнение называется дифференциальным?
- Перечислите известные вам типы дифференциальных уравнений первого порядка. Приведите примеры.
- Чем частное решение отличается от общего?
- Может ли решение дифференциального уравнения: а) быть конечным; б) быть представлено в виде
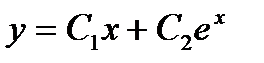 ?
? - Может ли ДУ первого порядка содержать: а) вторую производную искомой функции; б) искомую функцию; в) производную искомой функции; г) независимую переменную?
- Как записать в общем случае дифференциальное уравнение второго порядка?
- Что называется решением дифференциального уравнения второго порядка?
- Запишите в общем виде линейное дифференциальное уравнение второго порядка с постоянными коэффициентами.
- Что называется характеристическим уравнением?
- Напишите общее решение уравнения, когда его характеристическое уравнение не имеет действительных корней?
- Могут ли интегральные кривые ДУ: а) пересекаться; б) касаться?
- Может ли решение ДУ второго порядка: а) быть конечным; б) быть представлено в виде
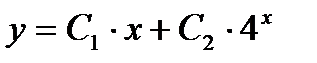 ?
?
Дата добавления: 2014-12-05; просмотров: 3020;
