Формула парабол (Симпсона)
Если заменить график функции у = f(x) на каждом отрезке [a;b] разбиения не отрезками прямых, как в методах трапеций и прямоугольников, а дугами парабол, то получим более точную формулу приближенного вычисления интеграла.
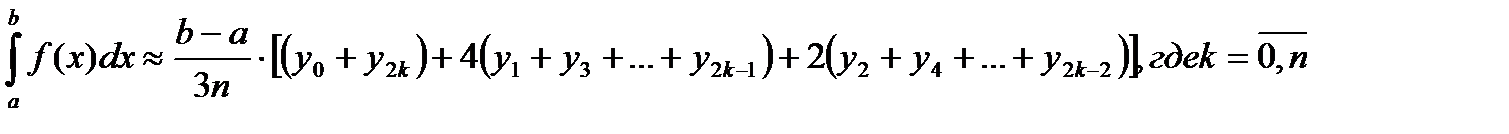 -(3)- формула Симпсона.
-(3)- формула Симпсона.
Задача. Вычислите четырьмя методами интеграл  ,
, 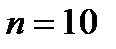
Решение.
1).По формуле Ньютона-Лейбница: 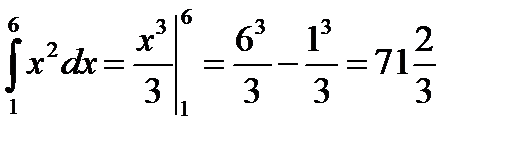
2) Методом прямоугольников.
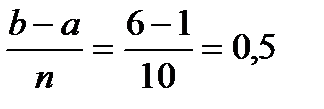
| x | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | 5,5 | 6 |
| y=x2 | 1 | 2,25 | 4 | 6,25 | 9 | 12,25 | 16 | 20,25 | 25 | 30,25 | 36 |
| yi | 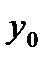
| 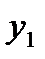
| 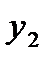
| 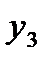
| 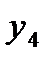
| 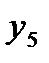
| 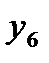
| 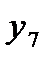
| 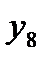
| 
| 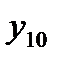
|
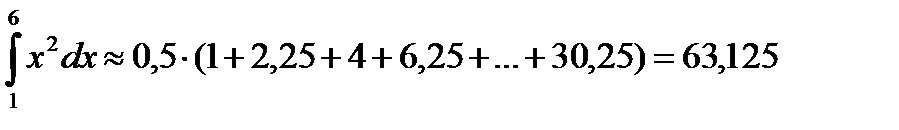
3) Методом трапеций.
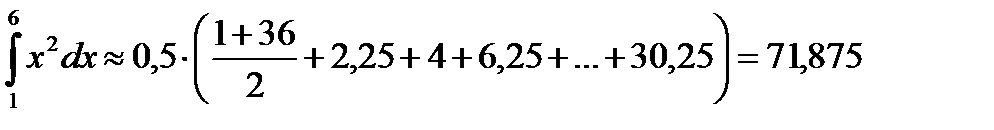
4) Методом Симпсона.
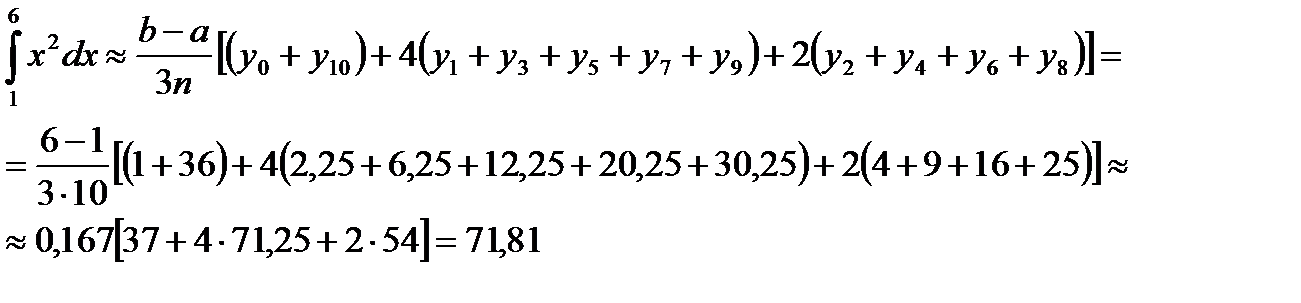
Содержание работы
Задание 1. Вычислите интеграл по формуле Ньютона – Лейбница:
1.1 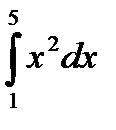 1.2
1.2 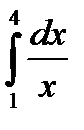 1.3
1.3 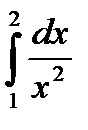 1.4
1.4 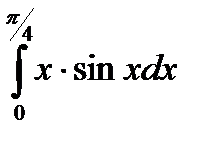 1.5
1.5 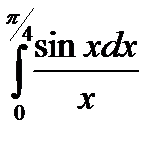
Задание 2. Вычислите приближенно интегралы из задания №1 используя формулу прямоугольников с точностью до 0,001 приняв n=8
Задание 3. Вычислите приближенно интегралы из задания №1 используя формулу трапеций с точностью до 0,001 приняв n=8
Задание 4. Вычислите приближенно интегралы из задания №1 используя формулу Симпсона с точностью до 0,001 приняв n=8
Вопросы для самоконтроля
- Что называется первообразной для данной функции. Приведите примеры.
- Что называется определенным интегралом от данной функции.
- Может ли значение определенного интеграла быть отрицательным?
- Для каких интегралов можно использовать методы приближенного вычисления?
- Какой из методов приближенного вычисления интегралов наиболее точный?
Дата добавления: 2014-12-05; просмотров: 1480;
