Численное дифференцирование.
Вычисление производных заданных функций проводится обычно по хорошо известным правилам и формулам дифференцирования. При этом получается аналитическое выражение для производной функции. Подстановка в полученное выражение любого аргумента, принадлежащего области допустимых значений, позволяет вычислить искомое значение производной функции. Если же функции заданы таблично, алгоритмически или очень сложной формулой с использованием специальных функций, то, как правило, прибегают к численному дифференцированию. Целью численного дифференцирования является расчет значения производной 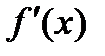 функции
функции 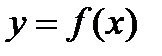 в определенной точке x.
в определенной точке x.
Дифференцируя полином (1) по переменной x, получим 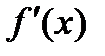 , при повторной процедуре -
, при повторной процедуре - 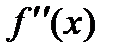 и т.д.
и т.д.
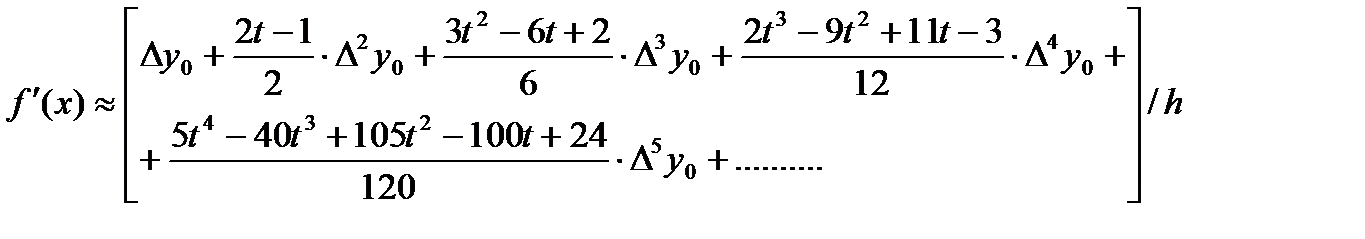 (3) первый интерполяционный полином Ньютона;
(3) первый интерполяционный полином Ньютона;
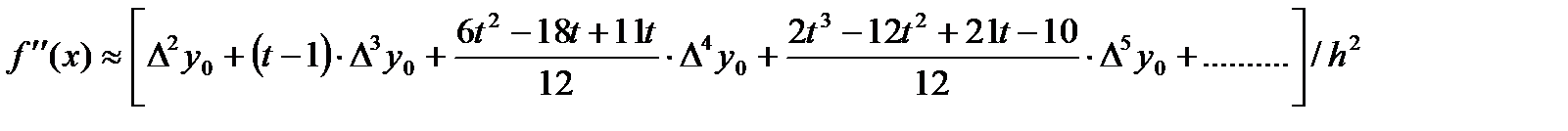 -(4) второй интерполяционный полином Ньютона;
-(4) второй интерполяционный полином Ньютона;
Если требуется вычислить значение первой или второй производной в каком – либо узле таблицы, то достаточно положить t=0 и из формул (3) и (4) получим следующие полезные формулы:
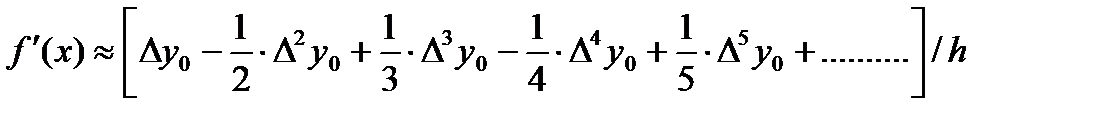 -(5) и
-(5) и
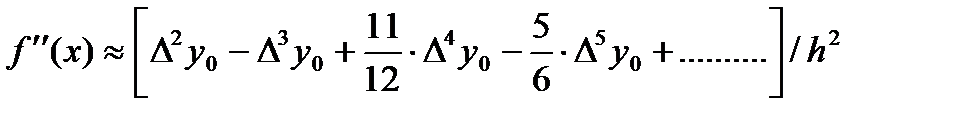 -(6)
-(6)
Погрешность всех формул определяется абсолютной величиной первого из отбрасываемых членов.
Пример 3. Некоторая функция f(x) задана таблицей.
| x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | |
| y | 0,4992 | 0,9933 | 1,4776 | 1,9471 | 2,3971 | 2,8232 | 3,2211 |
Вычислите первую производную 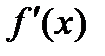 и вторую производную
и вторую производную 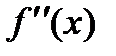 данной функции в точке x=0,24.
данной функции в точке x=0,24.
Решение. Ближайшим слева к числу 0,24 является узел 0,2. Его и выбираем за 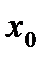 .
.
Составим таблицу разностей:
| x | y | 
| 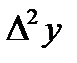
| 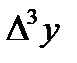
| 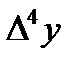
| 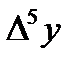
|
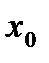 =0,2 =0,2
|  =0,9933 =0,9933
| |||||
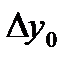 =0,4843 =0,4843
| ||||||
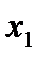 =0,3 =0,3
| 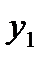 =1,4776 =1,4776
| 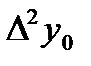 =-0,0148 =-0,0148
| ||||
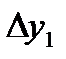 =0,4695 =0,4695
| 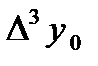 =-0,0047 =-0,0047
| |||||
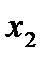 =0,4 =0,4
| 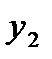 =1,9471 =1,9471
| 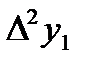 =-0,0195 =-0,0195
| 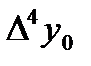 =0,0003 =0,0003
| |||
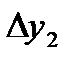 =0,4500 =0,4500
| 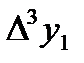 =-0,0044 =-0,0044
| 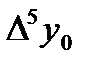 =-0,0002 =-0,0002
| ||||
 =0,5 =0,5
| 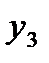 =2,3971 =2,3971
| 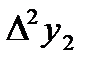 =-0,0239 =-0,0239
| 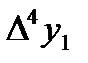 =0,0001 =0,0001
| |||
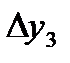 =0,4261 =0,4261
| 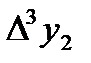 =-0,0043 =-0,0043
| |||||
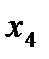 =0,6 =0,6
| 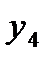 =2,8232 =2,8232
| 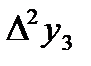 =-0,0282 =-0,0282
| ||||
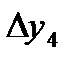 =0,3979 =0,3979
| ||||||
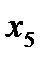 =0,7 =0,7
| 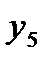 =3,2211 =3,2211
|
По первому интерполяционному полиному Ньютона (3), где 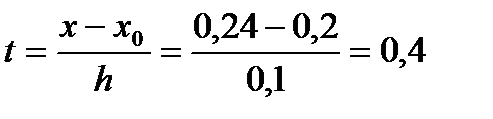 имеем:
имеем:
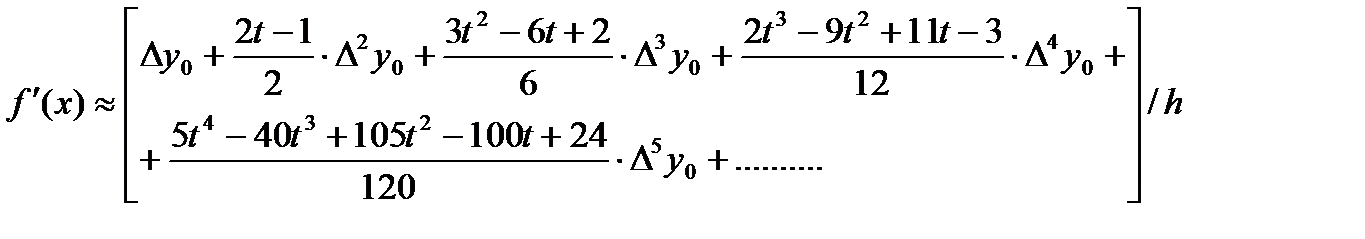 =
=
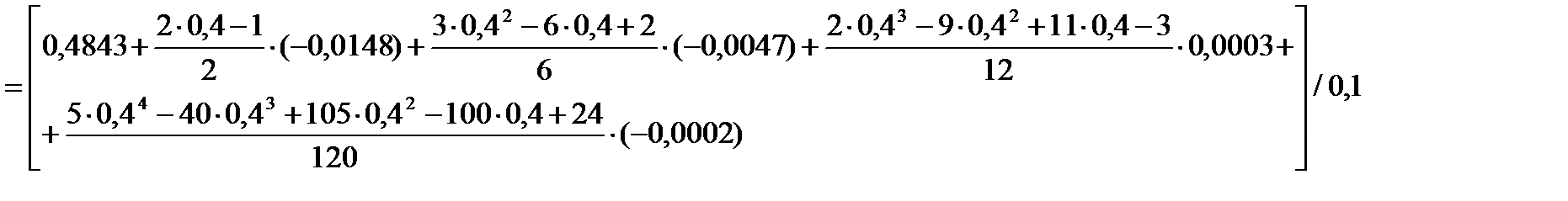
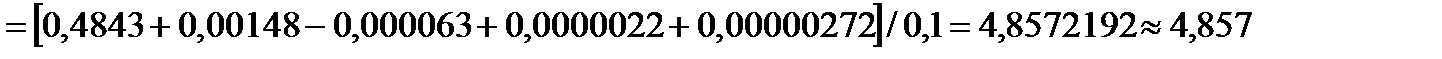
По первому интерполяционному полиному Ньютона (4):
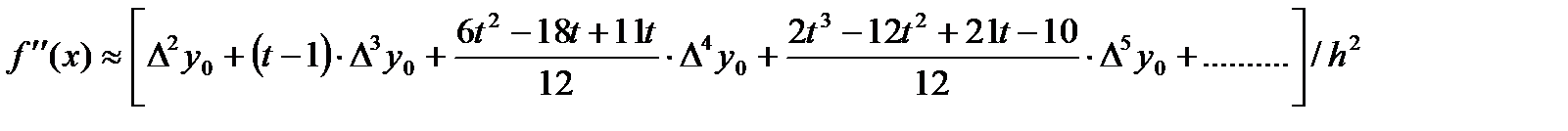 =
=
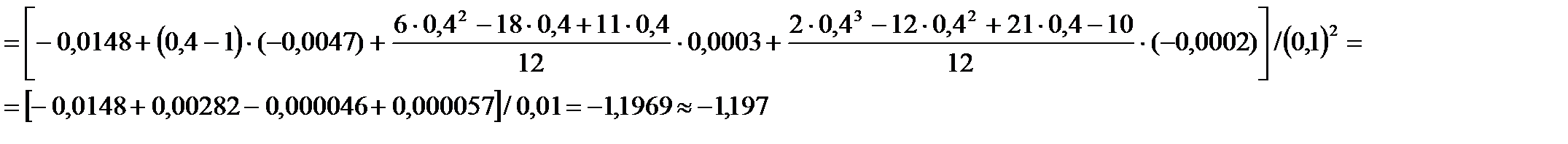 Итак,
Итак, 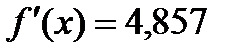 ,
, 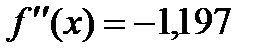 .
.
Содержание работы
Задание 1. Составить интерполяционный многочлен Ньютона для функции, заданной таблицей1.1
| x | |||||
| y |
1.2
| x | |||||
| y |
Задание 2. Известны значения некоторой функции f(x) в отдельных точках. Пользуясь интерполяционной формулой Ньютона, вычислите f(2,3):
2.1 f(1)=1,00; f(2)=0,25; f(3)=0,11; f(4)=0,06; f(5)=0,04; f(6)=0,03; f(7)=0,02
2.2 f(1)=2,00; f(2)=0,50; f(3)=0,22; f(4)=0,125; f(5)=0,08; f(6)=0,06; f(7)=0,04
Дата добавления: 2014-12-05; просмотров: 1546;
