Способы интерполяции. Интерполяционная формула Ньютона.
Пусть 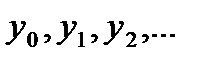 - значения некоторой функции
- значения некоторой функции 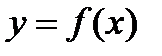 , соответствующие равноотстоящим значениям аргумента
, соответствующие равноотстоящим значениям аргумента 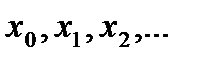 , т.е.
, т.е. 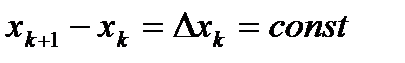 .
.
Введем обозначения:
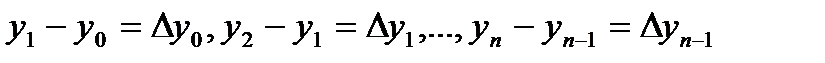 - разности первого порядка данной функции;
- разности первого порядка данной функции;
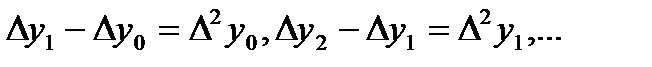 - разности второго порядка данной функции;
- разности второго порядка данной функции;
……….
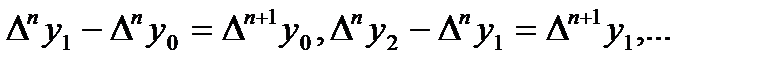 - разности (n+1)-го порядка данной функции.
- разности (n+1)-го порядка данной функции.
Запишем таблицу разностей:
| x | y | 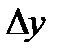
| 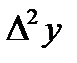
| 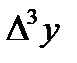
| 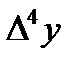
|
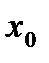
| 
| ||||
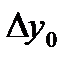
| |||||
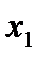
| 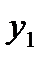
| 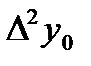
| |||
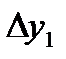
| 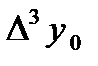
| ||||
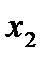
| 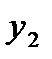
| 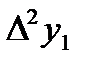
| 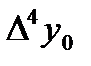
| ||
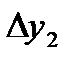
| 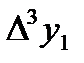
| ||||

| 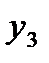
| 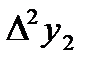
| |||
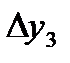
| |||||
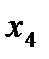
| 
| ||||
| … |
Если считать n – не только целое и положительное число, а может быть любым (n=t), то интерполяционная формула Ньютона выглядит так:
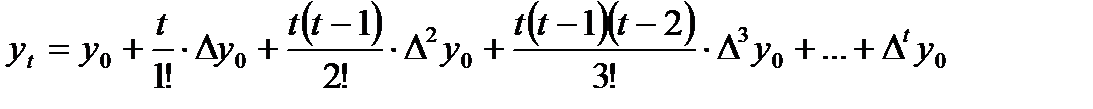 (1)- интерполяционная ф-ла Ньютона.
(1)- интерполяционная ф-ла Ньютона.
Мы получили такую функцию от t, которая при t=0 обращается в y0, при t=1 обращается в y1, при t=2 в y2 и т.д. Так как каждое последующее значение x при постоянном шаге h определяется равенством 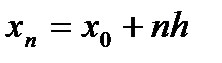 , то
, то 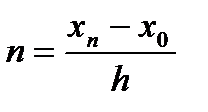 . Тогда полагая
. Тогда полагая 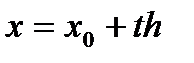 , т.е.
, т.е. 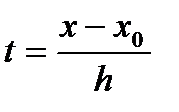 , приведем формулу(1)к виду
, приведем формулу(1)к виду 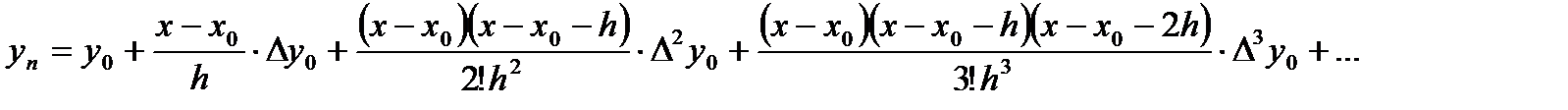 (2)
(2)
Пример1. Составить интерполяционный многочлен Ньютона для функции, заданной таблицей
| x | |||||
| y |
Решение: Составим таблицу разностей:
| x | y | 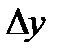
| 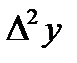
| 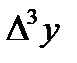
|
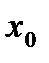 =1 =1
|  =3 =3
| |||
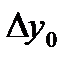 =7-3=4 =7-3=4
| ||||
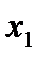 =2 =2
| 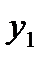 =7 =7
| 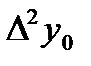 =6-4=2 =6-4=2
| ||
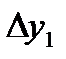 =13-7=6 =13-7=6
| 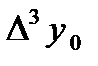 =2-2=0 =2-2=0
| |||
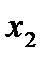 =3 =3
| 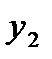 =13 =13
| 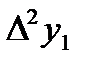 =8-6=2 =8-6=2
| ||
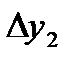 =21-13=8 =21-13=8
| 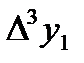 =2-2=0 =2-2=0
| |||
 =4 =4
| 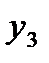 =21 =21
| 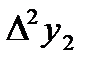 =10-8=2 =10-8=2
| ||
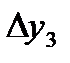 =31-21=10 =31-21=10
| ||||
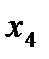 =5 =5
| 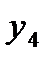 =31 =31
|
Здесь 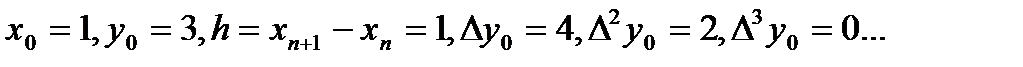 Подставим указанные значения в (2):
Подставим указанные значения в (2): 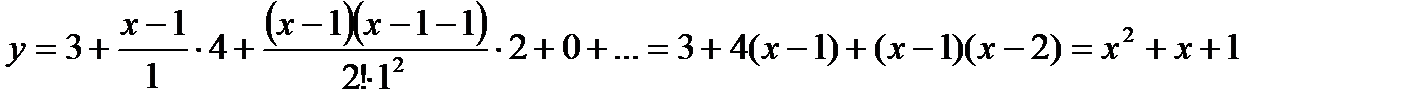 ,
,
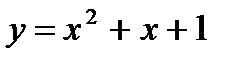 - интерполяционный многочлен Ньютона.
- интерполяционный многочлен Ньютона.
Пример 2. Даны десятичные логарифмы чисел: lg2,0=0,30103, lg2,1=0,32222, lg2,2=0,34242, lg2,3=0,36173, lg2,4=0,38021, lg2,5=0,39794. Пользуясь интерполяционной формулой Ньютона, найти lg2,03.
Решение. Составим таблицу разностей:
| x | y | 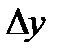
| 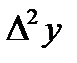
| 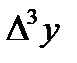
| 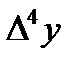
| 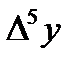
|
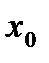 =2,0 =2,0
|  =0,30103 =0,30103
| |||||
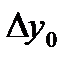 =0,02119 =0,02119
| ||||||
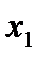 =2,1 =2,1
| 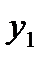 =0,32222 =0,32222
| 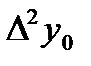 =-0,00099 =-0,00099
| ||||
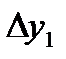 =0,02020 =0,02020
| 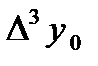 =0,0001 =0,0001
| |||||
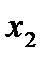 =2,2 =2,2
| 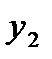 =0,34242 =0,34242
| 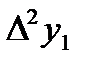 =-0,00089 =-0,00089
| 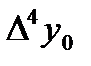 =-0,00004 =-0,00004
| |||
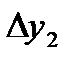 =0,1931 =0,1931
| 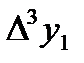 =0,00006 =0,00006
| 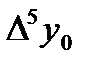 =-0,00006 =-0,00006
| ||||
 =2,3 =2,3
| 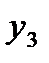 =0,36173 =0,36173
| 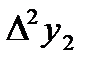 =-0,00083 =-0,00083
| 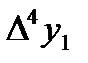 =-0,00002 =-0,00002
| |||
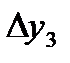 =0,01848 =0,01848
| 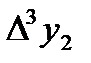 =0,00008 =0,00008
| |||||
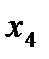 =2,4 =2,4
| 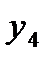 =0,38021 =0,38021
| 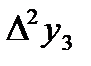 =-0,00075 =-0,00075
| ||||
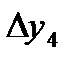 =0,1773 =0,1773
| ||||||
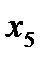 =2,5 =2,5
| 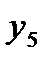 =0,39794 =0,39794
|
Здесь
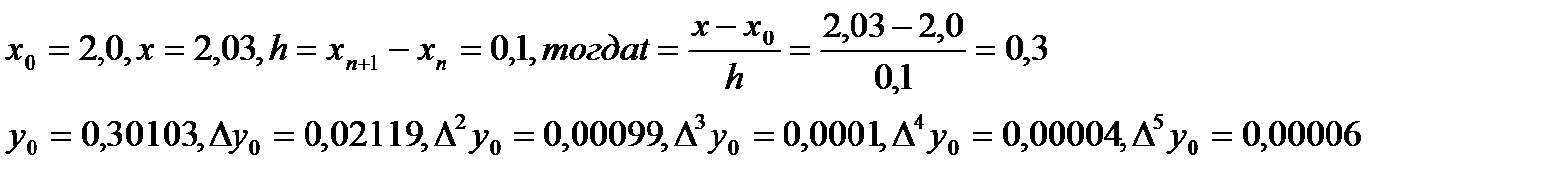
Подставим указанные значения в (1):
 Итак, lg2,03=0,30750
Итак, lg2,03=0,30750
Дата добавления: 2014-12-05; просмотров: 1505;
