Тема 7. Ряды

Бесконечным рядом (рядом) называется выражение вида

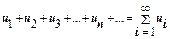
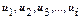, где – члены ряда;

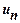– n-й или общий член ряда.

Если члены ряда:

— числа, то ряд называется числовым;

— числа одного знака, то ряд называется знакопостоянным;

— числа разных знаков, то ряд называется знакопеременным;

— положительные числа, то ряд называется знакоположительным;

— числа, знаки которых строго чередуются, то ряд называется знакочередующимся;

— функции, то ряд называется функциональным;

— степени x, то ряд называется степенным;

— тригонометрические функции, то ряд называется тригонометрическим.

Пусть мы имеем числовую последовательность a₁, a₂, a₃,…a_n, …, где a_kєR, k=1,2, ...

Числовой ряд – это сумма членов числовой последовательности вида

.

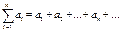Частичная сумма числового ряда – это сумма вида S_n=a₁+a₂+…a_n , где n - некоторое натуральное число. S_n называют также n-ой частичной суммой числового ряда.

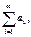Частичные суммы S₁,S₂,…, S_n,…образуют бесконечную последовательность частичных сумм числового ряда.

Числовой ряд называется сходящимся, если существует конечный предел последовательности частичных сумм

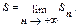Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд называется расходящимся.

Суммой сходящегося числового ряда называется предел последовательности его частичных сумм.

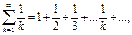Сумма вида

называется гармоническим числовым рядом.

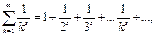Сумма вида

где s – некоторое действительное число, называется обобщенно- гармоническим числовым рядом.

1. Гармонический ряд является расходящимся.

2. Сумма геометрической прогрессии вида

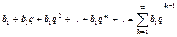со знаменателем q является сходящимся числовым рядом, если ׀q׀<1, и расходящимся при ׀ q ׀ ≤ 1.

3. Обобщенно-гармонический ряд сходится при s > 1 и расходится приs≤1.