Схема исследования функции двух переменных на экстремум.

1) Найти частные производные 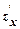и .

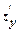2) Решить систему уравнени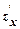й = 0 и 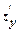= 0; найти стационарные точки функции.

3) Найти частные производные второго порядка, вычислить их значения в каждой стационарной точке, и с помощью достаточного условия сделать вывод о наличии экстремумов.

4) Найти значения экстремумов функции.

Пример 2. Найти экстремум функции z = 2х³+2у³ − 36ху + 430.

Р е ш е н и е.

1) Находим частные производные 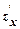= 6х² − 36у и 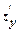= 6у² − 36х.

2) Стационарные точки находим из системы уравнений

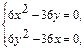
имеющей два решения (0;0) (6;6).

3) Находим частные производные второго порядка :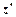

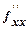= 12x, 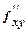= = 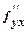- 36 и 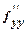=12y.

Для каждой пары решений определим числа А, В, С и Δ.

Для первой пары решений:А = 0; В = - 36; С=0, а потому Δ = АС − В²= - 36².

Так как Δ<0, то при х=0, у=0 функция не имеет экстремума (ни максимума, ни минимума).

Для второй пары решений:А = 72; В = - 36; С=72, теперь число Δ = АС −В² = 72²- 36² = 3888.

Так как Δ>0, то при х=6, у=6 функция имеет экстремум. Учитывая, что А – число положительное, заключаем, что при этих значениях х и у имеет место минимум.

4) Чтобы определить минимальное значение функции, подставим в нее х = 6, у = 6 и получим z _min = - 2.