Частные производные.

Дадим аргументу х приращение Δх, аргументу у – приращение Δу. Тогда функция z = f (x,у) получит наращенное значение f (x + Δх, у + Δу). Величина z = f (x + Δх, у + Δу) – f (x,у) называется полным приращением функции в точке (х,у). Если задать только приращение аргумента х или только приращение аргумента у, то полученные приращения функции, соответственно 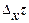= f (x + Δх, у) – f (x,у) и 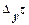= f (x , у + Δу) – f (x,у), называются частными.

Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при стремлении последнего к нулю (если этот предел существует), т.е.

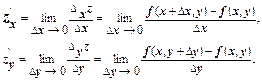
Пример 1. Найти частные производные функции z = ху².

Р ш е н и е. Чтобы найти частную производную по х, считаем у постоянной величиной. Таким образом: 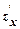= у². Аналогично, дифференцируя по у, считаем х постоянной величиной, т.е. 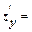2ху.