Экстремум функции нескольких переменных.

Как и в случае одной переменной, функция z = f (x,у) имеет узловые, определяющие структуру графика, точки.

Точка М₀ (х₀, у₀) называется точкой максимума (минимума) функции z = f (x,у), если существует окрестность точки М такая, что для всех точек (х, у) из этой окрестности выполняется неравенство:

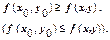
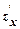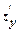Теорема (необходимое условие экстремума). Пусть точка М₀ (х₀, у₀) есть точка экстремума дифференцируемой функции z = f (x,у). Тогда частные производные и в этой точке равны нулю.

Если частные производные 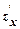и 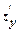сами являются дифференцируемыми функциями, то можно найти также и их частные производные, которые называются частными производными второго порядка ( 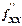, 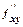= 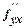и ).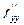

Теорема (достаточное условие экстремума). Пусть функция z = f (x,у):

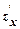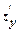1) определена в некоторой окрестности стационарной точки (х₀,у₀), в которой = 0 и = 0;

2) имеет в этой точке непрерывные частные производные второго порядка 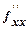(х₀, у₀) =А, 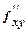(х₀, у₀) = 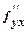(х₀, у₀) = В и 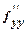(х₀, у₀) =С.

Тогда, если Δ=АС-В²>0, то в точке(х₀, у₀) функция имеет экстремум, причем, если А<0, – максимум, если А>0, – минимум. В случае Δ= АС-В² <0 функция экстремума не имеет. Если Δ =АС-В² =0, то вопрос о наличии экстремума остается открытым и требует дополнительных исследований.