Задача о вычислении площади криволинейной трапеции

Найдём площадь фигуры, которая ограничена осью абсцисс, отрезками прямых и параллельными оси ординат, и графиком функции 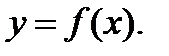Такая фигура называется криволинейной трапецией (рис. 1). Боковые отрезки могут вырождаться в точки. Например, фигуры, изображенные на рис. 2, - частные случаи криволинейных трапеций.

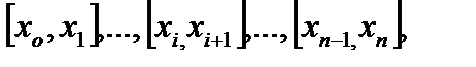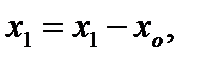Разобьём отрезок точками на (не обязательно равных) отрезков длины которых D D D D Их сумма составляет отрезок В точках деления проведем отрезки, перпендикулярные оси абсцисс до пересечения с графиком функции Криволинейная трапеция разобьётся на

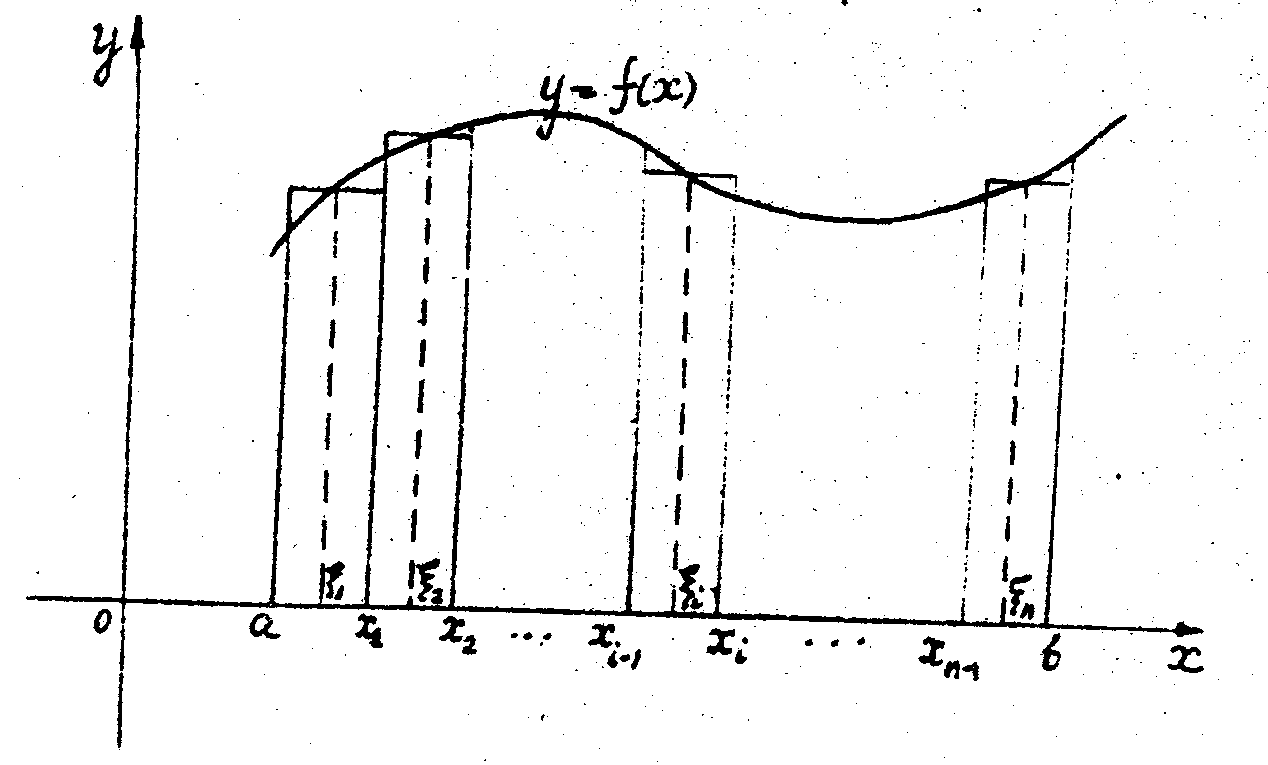
узких криволинейных трапеций (см. рис. 3).

Рис. 3.

На каждом отрезке построим прямоугольник, основание которого D 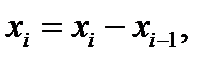а высота

равна значению функции в произвольно выбранной точке 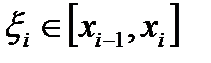в частных случаях она может совпадать с началом или концом данного отрезка). Площадь его равна D

Сумма площадей таких прямоугольников, построенных на всех отрезках равная

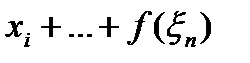D D 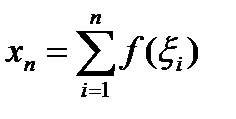D D выражает площадь ступенчатой фигуры (рис. 3) или приближенно площадь криволинейной трапеции. С увеличением числа точек деления эта сумма все точнее выражает площадь криволинейной трапеции, если длина максимального из отрезков уменьшается. Поэтому за площадь 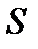криволинейной трапеции принимается предел суммы 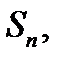т.е.

Можно доказать, что если функция непрерывна на отрезке то этот предел существует и не зависит ни от способа разбиения отрезка на малые отрезки, ни от выбора точек на них. Следовательно, если функция непрерывна на 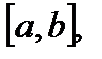то площадь криволинейной трапеции существует.