Определенный интеграл. Формула Ньютона-Лейбница
Выше было показано, что вычисление площади плоской фигуры свелось к нахождению предела особого рода сумм (1). Решение многих других задач математики, естествознания и техники приводит к вычислению пределов такого же рода сумм. Это даёт основание для следующего определения.
Определение. Пусть на отрезке 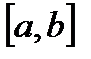 задана функция
задана функция  Разобьём отрезок
Разобьём отрезок  точками
точками 
 на
на  более мелких отрезков
более мелких отрезков  Длины которых
Длины которых 
На каждом из этих отрезков выберем по точке 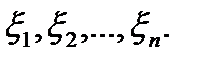
Длину наибольшего отрезка обозначим через 
Определенным интегралом от функции 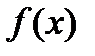 по отрезку
по отрезку  называется
называется
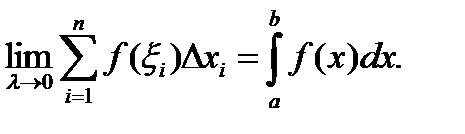 (1)
(1)
Выражение, стоящее под знаком предела, называется интегральной суммой для функции 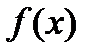 по отрезку
по отрезку 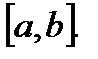 Числа
Числа  и
и 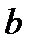 называются нижним и верхним пределами интегрирования соответственно.
называются нижним и верхним пределами интегрирования соответственно.
Из задачи о вычислении площади криволинейной трапеции вытекает следующий геометрический смысл определённого интеграла: если 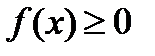 на
на  то
то
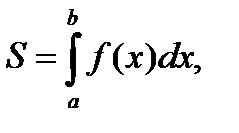
где  площадь криволинейной трапеции (рис. 1).
площадь криволинейной трапеции (рис. 1).
Если существует интеграл от функции 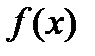 по отрезку
по отрезку 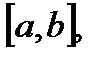 то функция
то функция  называется интегрируемой на
называется интегрируемой на 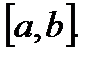
Справедливо следующее утверждение: если  непрерывна на отрезке
непрерывна на отрезке  то она интегрируема на
то она интегрируема на 
По определению будем считать, что
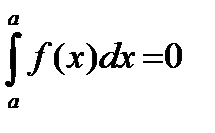 и
и 
Ключевую роль в вычислении определенных интегралов играет формула Ньютона-Лейбница, называемая основной формулой интегрального исчисления.
Теорема. Если 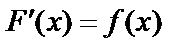 на
на  то
то
 (2)
(2)
Формула (2) показывает, что вычисление определенных интегралов сводится к вычислению первообразной (т.е. к вычислению неопределенных интегралов).
Для вычисления удобна сокращенная запись
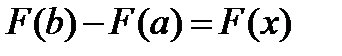

С помощью этого обозначения формулу (2) записывают так:

Дата добавления: 2014-12-30; просмотров: 1083;
