В несобственных интегралах с бесконечными пределами (т. е. симметричными интервалами интегрирования) нечётностью пользоваться НЕ СЛЕДУЕТ!!!

В этом состоит отличие от определенного интеграла. Там всегда можно смело записать:

,

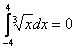а здесь так поступать – не следует. Почему? Потому что в ряде случаев, как, например, в рассмотренном примере, получится нонсенс. Если считать, что

,

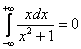то интеграл будет сходящимся (поскольку получено конечное число), но в то же время его часть:

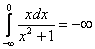
– расходится (как мы только что показали в решении). Тонкость же состоит в том, что несобственный интеграл

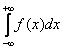
от нечетной функции 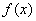, в принципе, может равняться нулю, но нельзя сразу записывать, что

.

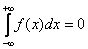Всегда представляем интеграл в виде двух интегралов и выполняем проверку на сходимость по стандартному алгоритму.

Как раз этой тонкости посвящен следующий пример для самостоятельного решения:

Пример 11

Вычислить несобственный интеграл или установить его расходимость.

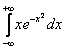
Полное решение и ответ в конце урока.