В интегралах рассматриваемого типа за всегда обозначается логарифм.

Технически оформление решения реализуется следующим образом, в столбик записываем:

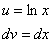
То есть, за 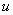мы обозначили логарифм, а за 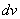– оставшуюся часть подынтегрального выражения.

Следующий этап: находим дифференциал :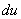

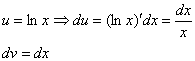
Дифференциал – это почти то же самое, что и производная, как его находить, мы уже разбирали на предыдущих уроках.

Теперь находим функцию 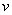. Для того чтобы найти функцию 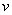необходимо проинтегрироватьправую часть нижнего равенства :

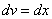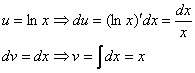
Теперь открываем наше решение и конструируем правую часть формулы: .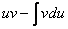
Вот кстати, и образец чистового решения с небольшими пометками:

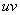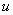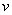Единственный момент, в произведении я сразу переставил местами и , так как множитель 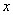принято записывать перед логарифмом.

Как видите, применение формулы интегрирования по частям, по сути дела, свело наше решение к двум простым интегралам.

Обратите внимание, что в ряде случаев сразу после применения формулы, под оставшимся интегралом обязательно проводится упрощение – в рассматриваемом примере мы сократили подынтегральное выражение на «икс».

Выполним проверку. Для этого нужно взять производную от ответа:

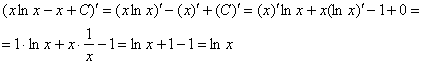
Получена исходная подынтегральная функция, значит, интеграл решён правильно.

В ходе проверки мы использовали правило дифференцирования произведения: 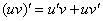. И это не случайно.