Но с точки зрения оформления задания метод подведения функции под знак дифференциала – гораздо короче.
Возникает вопрос. Если первый способ короче, то зачем тогда использовать метод замены? Дело в том, что для ряда интегралов не так-то просто «подогнать» функцию под знак дифференциала.
Пример 6
Найти неопределенный интеграл.
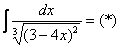
Проведем замену: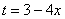 
(другую замену здесь трудно придумать)
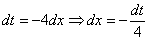
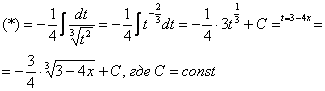
Как видите, в результате замены исходный интеграл значительно упростился – свёлся к обычной степенной функции. Это и есть цель замены – упростить интеграл.
Ленивые продвинутые люди запросто решат данный интеграл методом подведения функции под знак дифференциала:
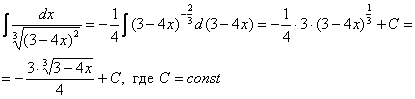
Другое дело, что такое решение очевидно далеко не для всех студентов. Кроме того, уже в этом примере использование метода подведения функции под знак дифференциала значительно повышает риск запутаться в решении.
Пример 7
Найти неопределенный интеграл. Выполнить проверку.
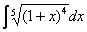
Это пример для самостоятельного решения. Ответ в конце урока.
Пример 8
Найти неопределенный интеграл.
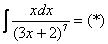
Замена: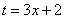 
Осталось выяснить, во что превратится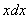 
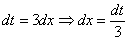
Хорошо,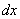 
мы выразили, но что делать с оставшимся в числителе «иксом»?!
Время от времени в ходе решения интегралов встречается следующий трюк: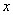 
мы выразим из той же замены !
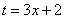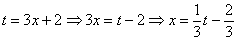
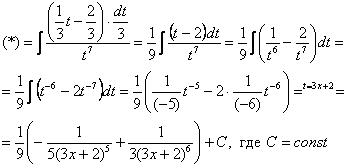
Готово.
Пример 9
Найти неопределенный интеграл.
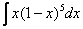
Это пример для самостоятельного решения. Ответ в конце урока.
Пример 10
Найти неопределенный интеграл.
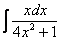
Наверняка некоторые обратили внимание, что в моей справочной таблице нет правила замены переменной. Сделано это сознательно. Правило внесло бы путаницу в объяснение и понимание, поскольку в вышерассмотренных примерах оно не фигурирует в явном виде.
Настало время рассказать об основной предпосылке использования метода замены переменной: в подынтегральном выражении должна находиться некоторая функция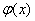
и её производная 
: 
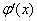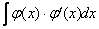(функции 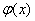, 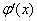могут быть и не в произведении)
В этой связи при нахождении интегралов довольно часто приходится заглядывать в таблицу производных.
В рассматриваемом примере замечаем, что степень числителя на единицу меньше степени знаменателя. В таблице производных находим формулу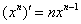 
, которая как раз понижает степень на единицу. А, значит, если обозначить за 
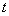знаменатель, то велики шансы, что числитель 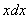превратится во что-нибудь хорошее.
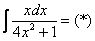
Замена: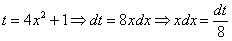 
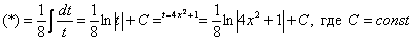
Кстати, здесь не так сложно подвести функцию под знак дифференциала:
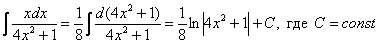
Следует отметить, что для дробей вроде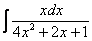 
, 
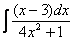такой фокус уже не пройдет (точнее говоря, применить нужно будет не только прием замены). Интегрировать некоторые дроби можно научиться на уроке Интегрирование некоторых дробей.
Вот еще пара типовых примеров для самостоятельного решения из той же оперы:
Пример 11
Найти неопределенный интеграл.
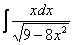
Пример 12
Найти неопределенный интеграл.
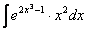
Решения в конце урока.
Пример 13
Найти неопределенный интеграл.
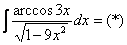
Смотрим в таблицу производных и находим наш арккосинус: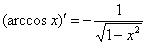 
. У нас в подынтегральном выражении находится арккосинус и нечто похожее на его производную.
Общее правило:
За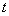 обозначаем саму функцию (а не её производную).
В данном случае: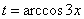 
. Осталось выяснить, во что превратится оставшаяся часть подынтегрального выражения 
.
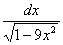В этом примере нахождение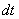 
я распишу подробно поскольку 
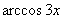– сложная функция.
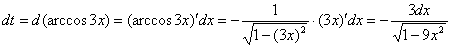
Или короче: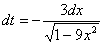 
По правилу пропорции выражаем нужный нам остаток: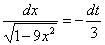 
Таким образом:
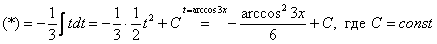
Вот здесь подвести функцию под знак дифференциала уже не так-то просто.
Пример 14
Найти неопределенный интеграл.
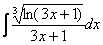
Пример для самостоятельного решения. Ответ совсем близко.
Внимательные читатели заметили, что я рассмотрел мало примеров с тригонометрическими функциями. И это не случайно, поскольку под интегралы от тригонометрических функцийотведён отдельный урок. Более того, на указанном уроке даны некоторые полезные ориентиры для замены переменной, что особенно актуально для чайников, которым не всегда и не сразу понятно, какую именно замену нужно проводить в том или ином интеграле. Также некоторые типы замен можно посмотреть в статье Определенный интеграл. Примеры решений.
Более опытные студенты могут ознакомиться с типовой заменой в интегралах с иррациональными функциями. Замена при интегрировании корней является специфической, и её техника выполнения отличается от той, которую мы рассмотрели на этом уроке.
Желаю успехов!
Решения и ответы:
Пример 3: Решение:
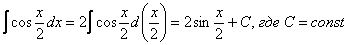
Пример 4: Решение:
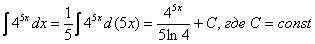
Пример 7: Решение:
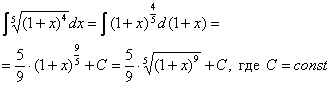
Пример 9: Решение:
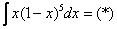
Замена: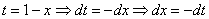 
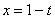
Пример 11: Решение:
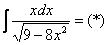
Проведем замену:
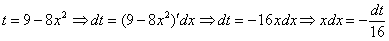
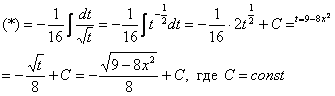
Пример 12: Решение:
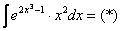
Проведем замену:
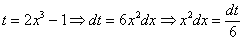
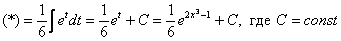
Пример 14: Решение:
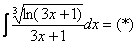
Проведем замену:
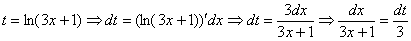
Дата добавления: 2014-11-29; просмотров: 1805;