Интегралы от тригонометрических функций, умноженных на многочлен
Общее правило: за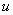
всегда обозначается многочлен
Пример 7
Найти неопределенный интеграл.
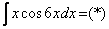
Интегрируем по частям:
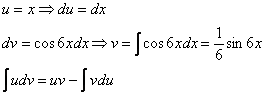
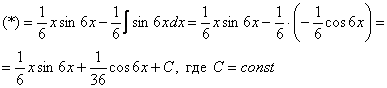
Хммм, …и комментировать нечего.
Пример 8
Найти неопределенный интеграл
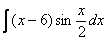
Это пример для самостоятельного решения
Пример 9
Найти неопределенный интеграл
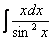
Еще один пример с дробью. Как и в двух предыдущих примерах за 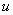обозначается многочлен.
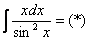
Интегрируем по частям:
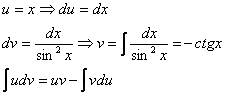
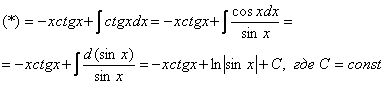
Если возникли трудности или недопонимание с нахождением интеграла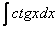 
, то рекомендую посетить урок Интегралы от тригонометрических функций.
Пример 10
Найти неопределенный интеграл
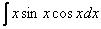
Это пример для самостоятельного решения.
Подсказка: перед использованием метода интегрирования по частям следует применить некоторую тригонометрическую формулу, которая превращает произведение двух тригонометрических функций в одну функцию. Формулу также можно использовать и в ходе применения метода интегрирования по частям, кому как удобнее.
Вот, пожалуй, и всё в данном параграфе. Почему-то вспомнилась строчка из гимна физмата «А синуса график волна за волной по оси абсцисс пробегает»….
Дата добавления: 2014-11-29; просмотров: 2040;