Графики обратных тригонометрических функций

Построим график арксинуса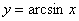

Перечислим основные свойства функции :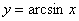

Область определения: 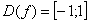, не существует значений вроде или

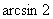
Область значений: 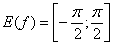, то есть, функция 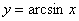ограничена.

Арксинус – функция нечетная, здесь минус опять же выносится: .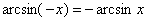

В практических вычислениях полезно помнить следующие значения арксинуса: 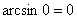, , 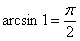. Другие распространенные значения арксинуса (а также других «арков») можно найти с помощью таблицы значений обратных тригонометрических функций.

Построим график арккосинуса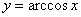

Очень похоже на арксинус, свойства функции сформулируйте самостоятельно. Остановлюсь на единственном моменте. В данной статье очень много разговоров шло о четности и нечетности функций, и, возможно, у некоторых сложилось впечатление, что функция обязательно должна быть четной или нечетной. В общем случае, это, конечно, не так. Чаще всего, функция, которая вам встретится на практике – «никакая». В частности, арккосинус не является четной или нечетной функцией, он как раз «никакой», или, строго говоря – это «функция общего вида по отношению к свойству чётности».

Построим график арктангенса

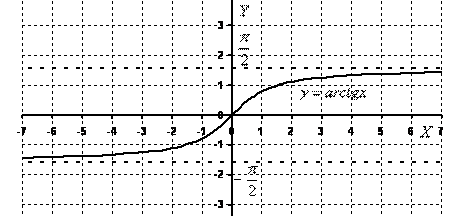
Всего лишь перевернутая ветка тангенса.

Перечислим основные свойства функции :

Область определения: 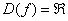, или «множество всех действительных чисел»

Область значений: 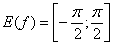, то есть, функция ограничена.

У рассматриваемой функции есть две асимптоты: , .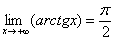

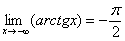Арктангенс – функция нечетная: .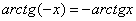

Самые «популярные» значения арктангенса, которые встречаются на практике, следующие: , .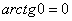

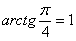К графику арккотангенса 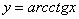приходиться обращаться значительно реже, но, тем не менее, вот его чертеж:

Свойства арккотангенса вы вполне сможете сформулировать самостоятельно. Отмечу, что арккотангенс, как и арккосинус, не является четной или нечетной функцией, а является «функцией общего вида по отношению к свойству чётности».

Пожалуй, для начала хватит. К этой странице придется частенько обращаться в ходе изучения самых различных разделов курса высшей математики.