График показательной функции
В данном параграфе я сразу рассмотрю экспоненциальную функцию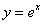 
, поскольку в задачах высшей математики в 95% случаев встречается именно экспонента.
Напоминаю, что 
– это иррациональное число: 
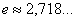, это потребуется при построении графика, который, собственно, я без церемоний и построю. Трёх точек, пожалуй, хватит:
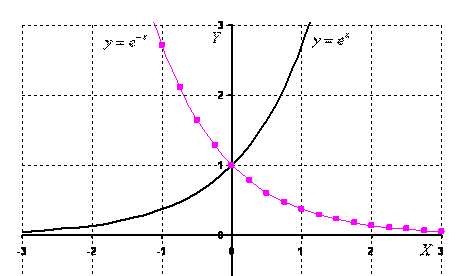
График функции 
пока оставим в покое, о нём позже.
Основные свойства функции :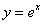
Область определения: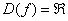 
– любое «икс».
Область значений: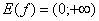 
. Обратите внимание, что ноль не включается в область значений. Экспонента – функция положительная, то есть для любого «икс» справедливо неравенство 
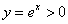, а сам график экспоненты полностью расположен в верхней полуплоскости.
Функция не ограничена сверху: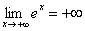 
, то есть, если мы начнем уходить по оси 
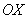вправо на плюс бесконечность, то соответствующие значения «игрек» стройным шагом будут тоже уходить вверх на 
по оси 
. Кстати, график экспоненциальной функции будет «взмывать» вверх на бесконечность очень быстро и круто, уже при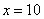 
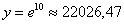
Исследуем поведение функции на минус бесконечности: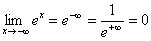 
. Таким образом, ось 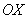является горизонтальной асимптотой для графика функции , если 
.
Принципиально такой же вид имеет любая показательная функция
, если 
. Функции 
, 
, 
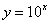будут отличаться только крутизной наклона графика, причем, чем больше основание, тем круче будет график.
Обратите внимание, что во всех случаях графики проходят через точку 
, то есть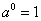 
.Это значение должен знать даже «двоечник».
Теперь рассмотрим случай, когда основание 
. Снова пример с экспонентой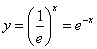 
– на чертеже соответствующий график прочерчен малиновым цветом? Что произошло? Ничего особенного – та же самая экспонента, только она «развернулась в другую сторону». Принципиально так же выглядят графики функций 
, 
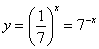и т. д. Должен сказать, что второй случай встречается на практике реже, но он встречается, поэтому я счел нужным включить его в данную статью.
Дата добавления: 2014-11-29; просмотров: 2308;