Графики тригонометрических функций

С чего начинаются тригонометрические мучения в школе? Правильно. С синуса

Построим график функции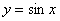

Данная линия называется синусоидой.

Напоминаю, что «пи» – это иррациональное число: 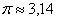, и в тригонометрии от него в глазах рябит.

Основные свойства функции :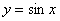

Данная функция является периодической с периодом 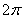. Что это значит? Посмотрим на отрезок 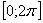. Слева и справа от него бесконечно повторяется точно такой же кусок графика.

Область определения: 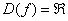, то есть для любого значения «икс» существует значение синуса.

Область значений: 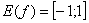. Функция 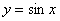является ограниченной: 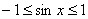, то есть, все «игреки» сидят строго в отрезке .
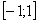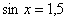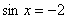Такого не бывает: или , точнее говоря, бывает, но указанные уравнения не имеют решения.

Синус – это функция нечетная, синусоида симметричная относительно начала координат, и справедлив следующий факт: . Таким образом, если в вычислениях встретится, например, , то минус терять здесь ни в коем случае нельзя! Он выносится:

Как ведет себя синус на бесконечности? Попробуем провести исследование с помощью пределов:
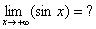, Чему равны такие пределы? Запомните, данных пределов не существует. По вполне понятным причинам, график синуса болтается как неприкаянный, то дойдет единицы, то уйдет к минус единице и так до бесконечности.

Вот вам пример, когда предела не существует. В высшей математике это можно встретить не очень часто, но такое понятие, как «предела не существует»– существует!

В практических вычислениях желательно (и даже обязательно) знать и помнить следующие значения синуса: , , .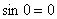

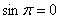Другие значения синуса (а также остальных тригонометрических функций) можно найти в методическом материале Тригонометрические таблицы.