Метод решения несобственного интеграла с точкой разрыва на отрезке интегрирования

Если честно, такой пример встречался в моей практике всего один раз (по крайне мне, вспомнил лишь один), поэтому я ограничусь только обзором.

Пример опять же будет в известной степени условным, первое, что в голову пришло. Рассмотрим несобственный интеграл

.

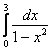На концах отрезка интегрирования всё хорошо. Но подынтегральная функция терпит бесконечный разрыв прямо на отрезке в точке x = 1. Подынтегральная функция является четной, но это не имеет никакого значения, поскольку отрезок интервал интегрирования не симметричен относительно нуля.

Метод уже состарился, как хмм… чешуя динозавра. Представим несобственный интеграл в виде суммы двух несобственных интегралов:

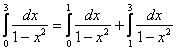
Интегралы правой части вам уже знакомы. А проговаривать алгоритм в третий раз не буду, смотрите предыдущие два параграфа)

Решения и ответы:

Пример 2: Решение:

Пример 5: Решение:

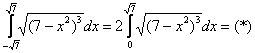
Проведем замену:


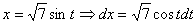
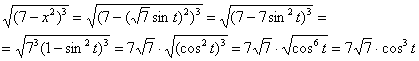
Новые пределы интегрирования:

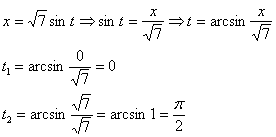
Пример 8: Решение:

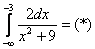
Подынтегральная функция непрерывна на интервале .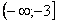

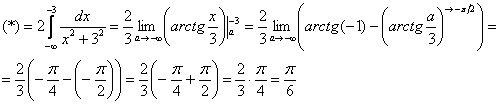
Пример 11: Решение:

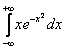
Подынтегральная функция непрерывна на всей числовой прямой.
Представим интеграл в виде суммы двух интегралов:

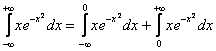
Проверим сходимость интегралов правой части:

Сходится.

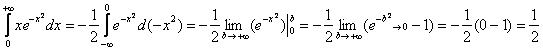
Сходится.
Оба интеграла сходятся, значит, сходится и весь интеграл:

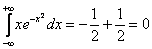
Ответ:

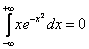
Примечание: Будет серьезной оплошностью сразу записать, что

,

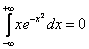пользуясь нечетностью подынтегральной функции и симметричностью интервала интегрирования. Стандартный алгоритм обязателен!!!

Пример 13: Решение:

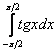
Подынтегральная функция терпит бесконечные разрывы в точках

.

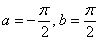Представим данный интеграл в виде суммы двух интегралов:

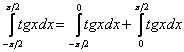
Исследуем сходимость интегралов правой части:

Несобственный интеграл расходится, значит, расходится и весь интеграл.

Интеграл

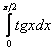можно уже не проверять.

Ответ:интеграл

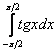– расходится