При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!

Чистовое оформление задания должно выглядеть примерно так:

Подынтегральная функция непрерывна на «полубесконечном» интервале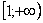

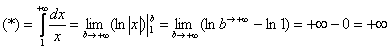
Несобственный интеграл расходится.

При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией на границах интервала.

Этим мы идентифицируем тип несобственного интеграла.

Если Вам встретится интеграл вроде

,

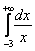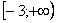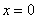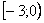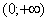то с вероятностью, близкой к 100%, можно сказать, что это опечатка. Здесь подынтегральная функция не является непрерывной на интервале интегрирования , она терпит разрыв в точке . Теоретически и практически допустимо вычислить два несобственных интеграла на интервалах и , а потом их сложить, но со здравой точки зрения такая вещь выглядит довольно абсурдно. Опечатка.

Иногда вследствие опечатки несобственного интеграла может вообще не существовать. Например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть интервала интегрирования вообще не войдёт в область определения подынтегральной функции.