Векторное произведение

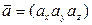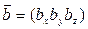Из двух векторов и можно образовать новый вектор:

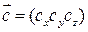, где

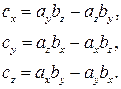
Модуль нового результирующего вектора находим по формуле:

.

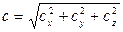Эта операция называется векторным произведением векторов 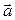и 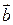и обозначается одним из символов 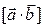или .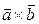

Также общеизвестна формула

,

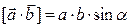где 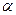- угол между векторам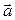и и .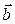

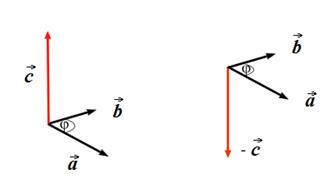
Направление вектора 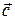можно найти, используя следующий прием. Мысленно совмещаем продольную ось буравчика (правого винта, штопора) с перпендикуляром к плоскости, в которой лежат перемножаемые векторы (в данном примере – векторы 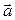и 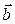). Затем начинаем вращать головку винта (ручку штопора) по направлению кратчайшего поворота от первого сомножителя ко второму, то есть от вектора 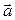к вектору 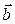. Направление движения тела винта и будет являться направлением вектора 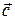. Этот прием называется правилом правого винта или правилом буравчика (см. рис.).