Производная и ее применения

Пусть функция у=f(х) определена в точках х и х₁ .Разность х₁ - х называется приращением аргумента, а разность f(х₁) - f(х) - приращением функциипри переходе от значения аргумента х к значению аргумента х₁. Приращение аргумента обозначают 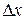, приращение функции обозначают 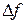или .

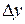Если существует предел отношения приращения функции 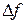к приращению аргумента 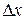при условии, что 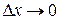, то функция у=f(х) называется дифференцируемой в точке х, а этот предел называется значением производной функции у=f(х) в точке х и обозначается 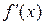или .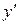

Операцию отыскания производной называют дифференцированием.