Координатный способ описания движения частицы

Радиус вектор частицы .

Скорость материальной точки .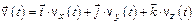

Ускорение материальной точки .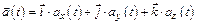

Здесь 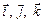– единичные векторы (орты), направленные по осям 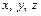соответственно (декартова система координат),

Если известны зависимости 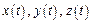, то можно определить:

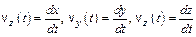– проекции скорости на оси ,

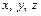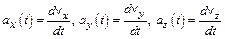– проекции ускорения на оси .

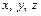Величина (модуль) радиса-вектора .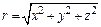

Величина (модуль) скорости .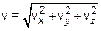

Величина (модуль) ускорения .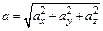

2-1. Радиус-вектор частицы зависит от времени по закону:

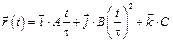. Найдите тангенс угла между вектором скорости 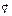и А) осью х Б) осью у в момент времени 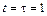с, если

А =В = С = 1 м.

2-2. Радиус-вектор частицы зависит от времени по закону:

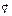. Найдите тангенс угла между вектором скорости и А) осью х;Б) осью z в момент времени 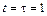с, если А = В = С = 1 м.

2-3. Радиус-вектор частицы зависит от времени по закону 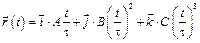. На каком расстоянии будет находиться частица в момент времени 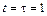с а) от оси х;б) от оси y; в) от оси z,

если А = В = С = 1 м.

2-4. Радиус-вектор частицы зависит от времени по закону

.

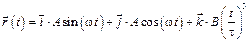Чему будет равна величина скорости частицы в момент времени 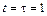с, если А = В = С = 1 м, 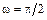рад/с.

2-5. Радиус-вектор частицы зависит от времени по закону 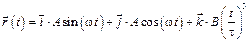. Чему будет равна величина начальной скорости частицы, если 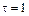с, А = В = 1 м, 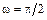рад/с.

2-6. Радиус-вектор частицы зависит от времени по закону 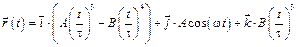. Через сколько секунд перпендикулярной оси х окажется а) скорость частицы; б) ускорение частицы если 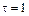с, А = В = 1 м, 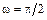рад/с.

2-7. Радиус-вектор частицы зависит от времени по закону .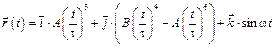

Через сколько секунд скорость частицы окажется перпендикулярной оси y, если 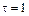с, А = В = 1 м, 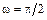рад/с.

2-8. Радиус-вектор частицы зависит от времени по закону .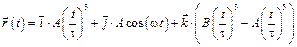

Через сколько секунд окажется перпендикулярной оси z,

а) скорость частицы; б) ускорение частицы,

если 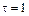с, А = В = 1 м, 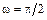рад/с.

2-9. Через сколько секунд ускорение частицы будет перпендикулярно оси y, если радиус-вектор частицы зависит от времени по закону 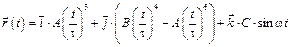, если 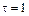с, А = В = С = 1 м, 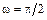рад/с.

2-10. Скорость частицы зависит от времени по закону

.

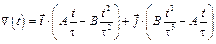Через сколько секунд ускорение частицы будет

а) параллельно оси х; б) перпендикулярно оси х; в) перпендикулярно оси y, если 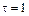с, А = В = 1 м/c.