Понятие комплексного числа

Прежде чем, мы перейдем к рассмотрению комплексных чисел, дам важный совет: не пытайтесь представить комплексное число «в жизни» – это всё равно, что пытаться представить четвертое измерение в нашем трехмерном пространстве. Если хотите, комплексное число – это двумерное число. И курить бессмысленно. … Так, кто тут улыбается? Видимо, действительно не помогло.

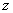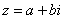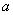Комплексным числом называется число вида , где и 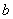– действительные числа, 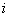– так называемая мнимая единица. Число 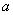называется действительной частью ( 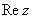)комплексного числа 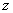, число 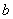называется мнимой частью ( 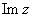) комплексного числа .

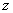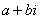– это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: 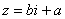или переставить мнимую единицу: 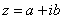– от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: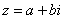

Чтобы всё было понятнее, сразу приведу геометрическую интерпретацию. Комплексные числа изображаются на комплексной плоскости:

Как упоминалось выше, буквой 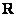принято обозначать множество действительных чисел. Множествоже комплексных чиселпринято обозначать «жирной» или утолщенной буквой 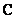. Поэтому на чертеже следует поставить букву 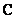, обозначая тот факт, что у нас комплексная плоскость.

Комплексная плоскость состоит из двух осей:
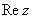– действительная ось
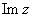– мнимая ось

Правила оформления чертежа практически такие же, как и для чертежа в декартовой системе координат (см. Графики и свойства элементарных функций). По осям нужно задать размерность, отмечаем:

ноль;

единицу по действительной оси;

мнимую единицу 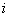по мнимой оси.

Не нужно проставлять все значения: …–3, –2, –1, 0, 1, 2, 3,… и .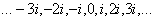

Да чего тут мелочиться, рассмотрим чисел десять.

Построим на комплексной плоскости следующие комплексные числа:
, ,
, ,
, , ,

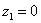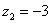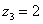
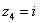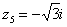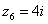
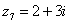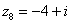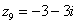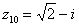
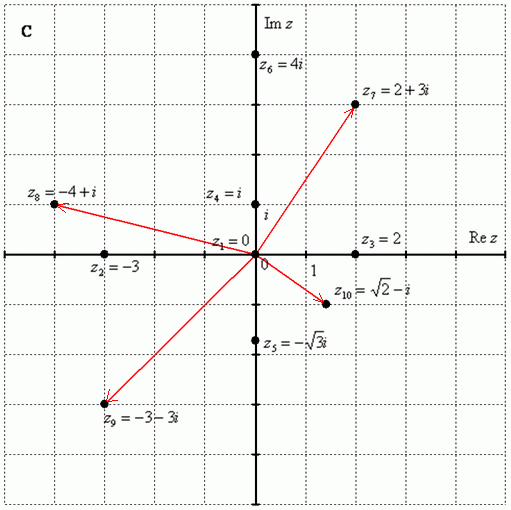
По какому принципу отмечены числа на комплексной плоскости, думаю, очевидно – комплексные числа отмечают точно так же, как мы отмечали точки еще в 5-6 классе на уроках геометрии.

Рассмотрим следующие комплексные числа: 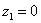, , 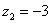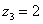. Вы скажете, да это же обыкновенные действительные числа! И будете почти правы. Действительные числа – это частный случай комплексных чисел. Действительная ось 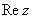обозначает в точности множество действительных чисел 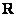, то есть на оси 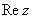сидят все наши «обычные» числа. Более строго утверждение можно сформулировать так: Множество действительных чисел 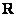является подмножеством множества комплексных чисел .

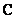Числа 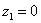, , 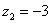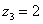– это комплексные числа с нулевой мнимой частью.

Числа 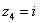, , 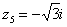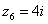– это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси .

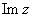В числах 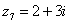, , 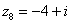, 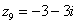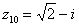и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не чертят, потому-что они сливаются с осями.