ПРЕДЕЛ ФУНКЦИИ
Пусть функция 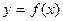 определена на некотором промежутке Х и пусть точка
определена на некотором промежутке Х и пусть точка 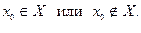
Определение 1.3.1. Число А называется пределом функции 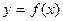 в точке
в точке 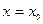 , если для любого числа
, если для любого числа  существует число
существует число  такое, что для всех
такое, что для всех  удовлетворяющих неравенству
удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство 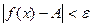 .
.
Пример 1. Используя определение предела функции, доказать, что  .
.
Решение. Возьмем любое  . Необходимо по этому
. Необходимо по этому  найти такое
найти такое  , при котором из неравенства
, при котором из неравенства 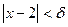 следовало бы неравенство
следовало бы неравенство  . Преобразуем последнее неравенство:
. Преобразуем последнее неравенство:
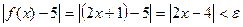 , или
, или  .
.
Отсюда видно, что если взять, например  , то для всех х, удовлетворяющих неравенству
, то для всех х, удовлетворяющих неравенству 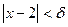 , выполняется требуемое неравенство
, выполняется требуемое неравенство  , а это и означает, что
, а это и означает, что  .
.
В частности, если 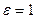 , то
, то 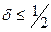 , если
, если  , то
, то  и т.д.
и т.д.
Раскрытие неопределенностей вида 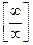 и
и 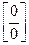 .
.
Если подстановка предельного значения вместо независимой переменной не дает значения предела, то имеет место неопределенность.
Для раскрытия неопределенности 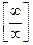 можно использовать те же приемы что и для последовательностей чисел.
можно использовать те же приемы что и для последовательностей чисел.
Пример 2. Вычислить предел 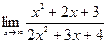
Решение: Имеем неопределенность вида 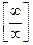 . Разделив на
. Разделив на 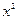 числитель и знаменатель дроби, получим:
числитель и знаменатель дроби, получим:
 , так как дроби
, так как дроби 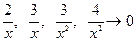 , при
, при 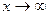 .
.
Неопределенность вида 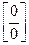 раскрывается путем разложения на множители выражений, стоящих в числителе и знаменателе дроби.
раскрывается путем разложения на множители выражений, стоящих в числителе и знаменателе дроби.
Пример 3. Вычислить предел 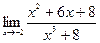 .
.
Решение: Имеем неопределенность вида 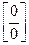 . Тогда получим:
. Тогда получим:
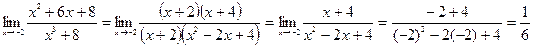
Пример 4. Вычислить предел 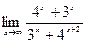 .
.
Решение: В числителе и знаменателе дроби стоит показательная функция 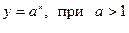 , которая стремится к бесконечности при
, которая стремится к бесконечности при 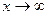 . Быстрее возрастает та функция, у которой основание больше, поэтому разделим числитель и знаменатель на
. Быстрее возрастает та функция, у которой основание больше, поэтому разделим числитель и знаменатель на  :
:
 .
.
Пример 5.Вычислить предел  .
.
Решение: Умножим числитель и знаменатель дроби на выражение, сопряженное числителю, то есть на 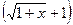 :
:
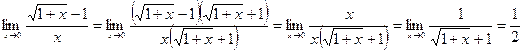 .
.
Раскрытие неопределенностей вида  .
.
Пример 6. Вычислить предел  .
.
Решение: Подставляя единицу в выражение, стоящее под знаком предела, получаем неопределенность типа  . Чтобы ее раскрыть, необходимо привести дроби к общему знаменателю и полученные выражения в числители и знаменатели разложить на множители.
. Чтобы ее раскрыть, необходимо привести дроби к общему знаменателю и полученные выражения в числители и знаменатели разложить на множители.
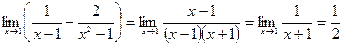 .
.
Пример 7. Вычислить предел 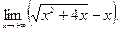 .
.
Решение: Имеем неопределенность вида  . Чтобы ее раскрыть, необходимо выражение, стоящее под знаком предела, домножить и разделить на сопряженное выражение, приводящее к формуле.
. Чтобы ее раскрыть, необходимо выражение, стоящее под знаком предела, домножить и разделить на сопряженное выражение, приводящее к формуле.
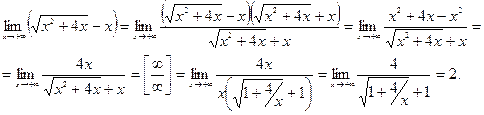
Дата добавления: 2014-12-04; просмотров: 1198;
