Упростим выражение, стоящее под модулем
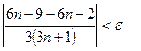 , получим
, получим 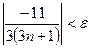 .
.
Учитывая, что под модулем стоит отрицательное число, получим 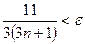 , следовательно
, следовательно 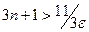 , и окончательно
, и окончательно
(**) 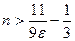 .
.
Если выполняется неравенство (**), то выполняется и неравенство (*). Найдем номер N(e)?
Очевидно, что если 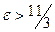 , то
, то 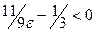 и неравенства (**) и (*) выполняются для всех п = 1,2,3,…, то есть N (e) = 0.
и неравенства (**) и (*) выполняются для всех п = 1,2,3,…, то есть N (e) = 0.
Если 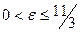 , то
, то 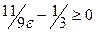 , и за номер N(e) можно взять целую часть [
, и за номер N(e) можно взять целую часть [  ], то есть N (e) = [
], то есть N (e) = [  ].
].
Основные свойства сходящихся последовательностей:
1. Сходящаяся последовательность имеет только один предел.
2. Сходящаяся последовательность ограничена.
3. Сумма (разность) сходящихся последовательностей íхпý и íупý есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностей íхпý и íупý.
4. Произведение сходящихся последовательностей íхпý и íупý есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей íхпý и íупý.
5. Частное двух сходящихся последовательностей íхпý и íупý при условии, что предел последовательности íупý отличен от нуля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей íхпý и íупý.
Вычисление пределов числовых последовательностей часто требует умения раскрывать неопределенности вида ¥¤¥. Если общий член последовательности представляет собой дробь с многочленами в числителе и знаменателе, надо разделить числитель и знаменатель дроби на пк - старшую степень знаменателя, и использовать свойства пределов.
Пример 2.
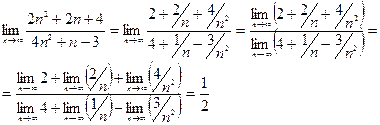
Для ряда примеров на раскрытие неопределенности типа ¥¤¥ необходима техника работы с дробными показателями.
Пример 3.
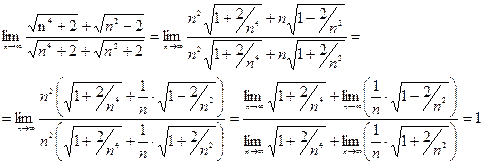
Чтобы раскрыть неопределенность типа « ¥ - ¥ », в ряде случаев рекомендуется выражение под знаком предела умножить и соответственно разделить на сопряженное ему выражение. Примеры сопряженных выражений:
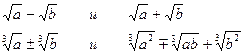
Пример 4.
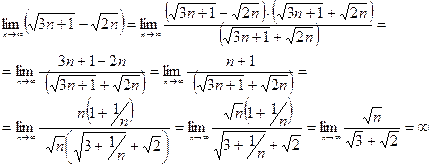
При раскрытии неопределенностей вида 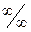 иногда помогает прием деления и числителя и знаменателя на выражение, которое растет быстрее при
иногда помогает прием деления и числителя и знаменателя на выражение, которое растет быстрее при 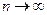 .
.
Дата добавления: 2014-12-04; просмотров: 1203;
