Два замечательных предела.
Первый замечательный предел.
Предел функции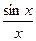 
в точке x=0 существует и равен единице, то есть:
Пример 8.Вычислить предел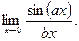 
Решение: Имеем неопределенность вида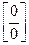 
. Преобразуем данную дробь таким образом, чтобы в знаменателе был аргумент синуса:
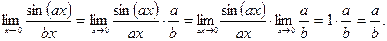
Пример 9.Вычислить предел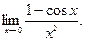 
Решение. Преобразуем данную дробь, используя тригонометрические формулы, а затем выполним предельный переход:
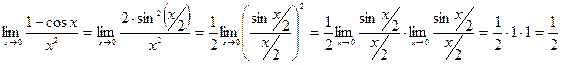
Пример 10.Вычислить предел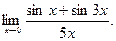 
Решение: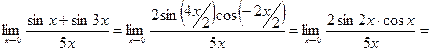 
.
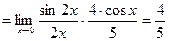Второй замечательный предел формулировался ранее в теме «Числовая последовательность и ее пределы». Тем не менее, сформулируем его еще раз:
Предел функции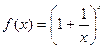 
при 
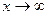существует и равен числу e, т. е.
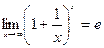
Пример 11.Вычислить предел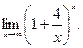 
Решение. Заменим переменную, приняв 
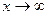. При и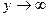 
последовательно получаем:
.
Пример 12.Вычислить предел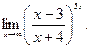 
Решение: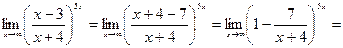 
.
Дата добавления: 2014-12-04; просмотров: 994;