ИДЗ-6. Вычисление пределов с использованием замечательных пределов
Вычислить пределы, применяя I и II замечательные пределы:
а) 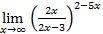 ; б)
; б) 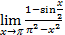 .
.
Решение: Выражения для I и II замечательного пределов есть, соответственно:
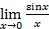 = 1;
= 1;
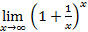 = e.
= e.
а) Путем несложных преобразований приведем данный предел к стандартному виду II замечательного предела:
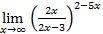 =
= 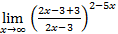 =
= 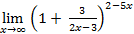 =
= 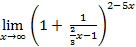 .
.
Для удобства выполним замену переменной под знаком предела. Обозначим  x – 1 = t. Тогда при x ® ¥ и новая переменная t ® ¥. Кроме того, x =
x – 1 = t. Тогда при x ® ¥ и новая переменная t ® ¥. Кроме того, x =  (t + 1) и 2 – 5x = 2 – 5×
(t + 1) и 2 – 5x = 2 – 5×  (t + 1) = 2 –
(t + 1) = 2 – 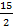 –
– 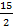 t = –
t = – 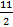 –
– 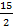 t. Продолжим выкладки:
t. Продолжим выкладки:
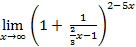 =
= 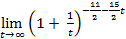 =
=
= 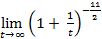 ×
× 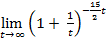 = 1×
= 1× 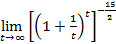 =
= 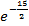 .
.
б) Приведем данный предел 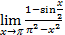 к стандартному виду I замечательного предела. Выполним замену переменной под знаком предела. Обозначим p – x = t. Тогда при x ® p новая переменная t ® 0. Кроме того,
к стандартному виду I замечательного предела. Выполним замену переменной под знаком предела. Обозначим p – x = t. Тогда при x ® p новая переменная t ® 0. Кроме того,
p2 – x2 = p2 – (p – t)2 = t(2p – t)
и
1 – sin  = 1 – sin
= 1 – sin 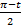 = 1 – sin
= 1 – sin 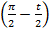 = 1 – cos
= 1 – cos  = 1 – (1 – 2sin2
= 1 – (1 – 2sin2  ) = 2sin2
) = 2sin2  .
.
Теперь
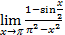 =
= 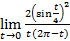 =
=  ×
× 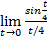 ×
× 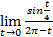 =
=  ×1×0 = 0.
×1×0 = 0.
Ответ: а) 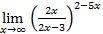 =
= 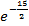 ; б)
; б) 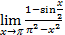 = 0.
= 0.
Дата добавления: 2014-12-06; просмотров: 1483;
