ИДЗ-5. Вычисление пределов с использованием теорем о пределах
Вычислить пределы, применяя теоремы о пределах:
а)  ; б)
; б)  ; в)
; в) 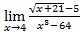 .
.
Решение: а) При x ® –2 числитель и знаменатель, как нетрудно убедиться, обращаются в нуль, давая под пределом неопределенность вида {0/0}. Поэтому в данном случае непосредственное применение теоремы о пределе отношения невозможно. Предварительно преобразуем дробь для избавления от неопределенности:
5x2 + 13x + 6 = (5x + 3)(x + 2); 3x2 + 2x – 8 = (3x – 4)(x + 2).
После простых преобразований возможно применение теорем о пределах:
 =
= 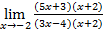 =
= 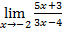 =
= 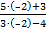 =
= 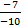 =
= 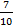 .
.
б) При n ® ¥ числитель и знаменатель обращаются в бесконечность, давая под пределом неопределенность вида {¥/¥}. Поэтому и здесь непосредственное применение теоремы о пределе отношения невозможно. Как и выше, необходимо предварительное преобразование дроби для избавления от неопределенности, для чего разделим и числитель и знаменатель на старшую степень выражения, в данном случае n4:
 =
= 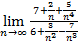 =
= 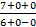 =
=  .
.
в) При x ® 4 числитель и знаменатель обращаются в нуль, давая под пределом неопределенность вида {0/0}. Поэтому непосредственное применение теоремы о пределе отношения невозможно. Необходимо предварительное преобразование дроби для избавления от неопределенности. Для этого числитель и знаменатель домножим на сопряженную сумму и разложим разность кубов в знаменателе на множители:
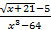 =
= 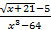 ×
× 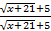 =
= 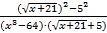 =
= 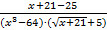 =
=
= 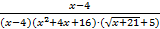 =
= 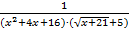 .
.
Полученное выражение уже не имеет особенности при x ® 4 и после простых преобразований возможно применение теорем о пределах:
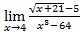 =
= 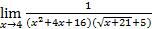 =
= 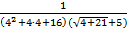 =
= 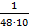 =
=  .
.
Ответ: а)  =
= 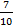 ; б)
; б)  =
=  ; в)
; в) 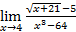 =
=  .
.
Дата добавления: 2014-12-06; просмотров: 1980;
