ИДЗ-8. Дифференцирование функций. Продифференцировать данные функции:
Продифференцировать данные функции:
а) y = 9x5 –  +
+ 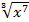 – 3x + 4; б) y = tg5(x+2)×arccos3x2; в) y =
– 3x + 4; б) y = tg5(x+2)×arccos3x2; в) y = 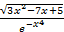 .
.
Решение: Выполним задание, используя теоремы о производных и таблицу производных.
а) y¢ = (9x5 –  +
+ 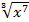 – 3x + 4)¢ = (9x5)¢ – (4x–3)¢ + (x7/3)¢ – (3x)¢ + (4)¢ =
– 3x + 4)¢ = (9x5)¢ – (4x–3)¢ + (x7/3)¢ – (3x)¢ + (4)¢ =
= 9×5x4 – 4×(–3)x–4 +  x4/3 – 3 + 0 = 45x4 +
x4/3 – 3 + 0 = 45x4 + 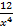 +
+  – 3.
– 3.
б) Заметим, что y¢ = (uv)¢ = u¢v + uv¢, где u = tg5(x+2) и v = arccos3x2. Вычислим производные для функций u(x) и v(x):
u¢ = (tg5(x+2))¢ = 5×tg4(x+2)×(tg(x+2))¢ = 5×tg4(x+2)×  = 5×tg4(x+2)×
= 5×tg4(x+2)×  ;
;
v¢ = (arccos3x2)¢ = – 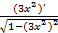 = –
= – 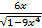 ;
;
Остается «собрать» окончательное выражение:
y¢ = u¢v + uv¢ = 5×tg4(x+2)×  ×arccos3x2 – tg5(x+2)×
×arccos3x2 – tg5(x+2)× 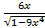 .
.
в) Как и в предыдущем примере, запишем y¢ = (uv)¢ = u¢v + uv¢, где u = 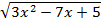 и v =
и v = 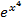 . Вычислим производные для функций u(x) и v(x):
. Вычислим производные для функций u(x) и v(x):
u¢ = ( 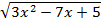 )¢ =
)¢ = 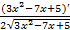 =
= 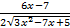 ;
;
v¢ = ( 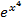 )¢ =
)¢ = 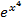 (x4)¢ = 4x3×
(x4)¢ = 4x3× 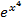 ;
;
Остается «собрать» окончательное выражение:
y¢ = u¢v + uv¢ = 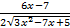 ×
× 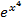 –
– 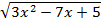 ×4x3×
×4x3× 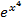 .
.
Ответ: а) y¢ = 45x4 + 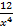 +
+  – 3; б) y¢ = 5×tg4(x+2)×
– 3; б) y¢ = 5×tg4(x+2)×  ×arccos3x2 – tg5(x+2)×
×arccos3x2 – tg5(x+2)× 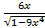 ; в) y¢ =
; в) y¢ = 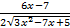 ×
× 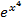 –
– 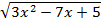 ×4x3×
×4x3× 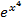 .
.
Дата добавления: 2014-12-06; просмотров: 2857;
