ИДЗ-11. Полное исследование функции и построение ее графика.

Провести полное исследование указанных функций и построить их графики:

а) y = 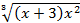; б) y = – .

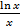Решение: Полное исследование функций и построение их графиков проведем, придерживаясь следующей примерной схемы:

1) Указать область D определения функции f(x);

2) Найти (если они существуют) точки разрыва функции, точки пересечения ее графика с осями координат и вертикальные асимптоты;

3) Установить наличие или отсутствие четности/нечетности, периодичности f(x);

4) Исследовать функцию на монотонность и экстремум;

5) Определить интервалы выпуклости и вогнутости, точки перегиба;

6) Найти наклонные (горизонтальные) асимптоты графика функции;

7) Произвести необходимые дополнительные вычисления, уточняющие ход f(x);

8) Построить график y = f(x) в масштабе, правильно отражающем установленные особенности поведения функции.

а) Проведем полное исследование функции y = f(x) = 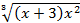, придерживаясь рекомендуемой схемы.

1. Функция f(x) определена для всех действительных x Î R, т.е. D = R.

2. Функция не имеет точек разрыва, т.е. является непрерывной всюду на области D своего определения. Функция пересекает ось Ox в точках x₀₁ = –3 и x₀₂ = 0, т.е. нулями функции y = f(x) = 0 являются точки x₀₁ = –3 и x₀₂ = 0. Функция пересекает ось Oy (здесь x = 0) в точке y = 0. Отсутствие точек разрыва функции указывает также на отсутствие вертикальных асимптот у графика y(x).

3. Функция f(x) не является четной или нечетной, не является периодической, т.е. является функцией общего вида.

4. Для исследования функции на монотонность и экстремум вычислим ее первую производную:

y¢ = ( )¢ = × = × = .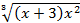

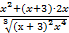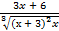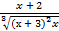Точками, подозрительными на экстремум (там, где производная y¢(x) равна нулю или не существует) являются точки x₁ = –3; x₂ = –2; x₃ = 0. Эти три особые точки разбивают область определения функции D на четыре (непересекающихся) интервала: D₁ = (–¥; –3), D₂ = (–3; –2), D₃ = (–2; 0), D₄ = (0; +¥). Изучим каждый из них.

Интервал D₁ = (–¥; –3). Здесь y¢ > 0 и функция y = f(x) возрастает.

Интервал D₂ = (–3; –2). Здесь y¢ > 0; функция y = f(x) возрастает.

Интервал D₃ = (–2; 0). Здесь y¢ < 0 и функция y = f(x) убывает.

Интервал D₄ = (0; +¥). Здесь y¢ > 0; функция y = f(x) возрастает.

Знак первой производной y¢(x) изменяется c «+» на «–» в точке x₂ = –2; в этой точке функция y = f(x) достигает (локального) максимума, равного y_max = f(–2) = 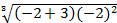= 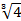» 1,587. В самой точке x₂ производная y¢(x₂ = –2) = 0.

Знак первой производной y¢(x) изменяется c «–» на «+» в точке x₃ = 0; в этой точке функция y = f(x) достигает (локального) минимума, равного y_min = 0. В самой точке x₂ производная y¢(x₂ = 0) ® ¥, т.е. касательная к графику функции y(x) в точке x₃ = 0 вертикальна.

В точке x₁ = –3 изменения знака первой производной не происходит, т.е. функция f(x) не имеет максимума или минимума. В самой точке x₁ производная y¢(x₁ = –3) ® ¥, т.е. касательная к графику функции y(x) в точке x₃ = 0 вертикальна.

5. Для определения интервалов выпуклости и вогнутости и точек перегиба вычислим вторую производную функции, как производную отношения:

y² = ( )¢ = = =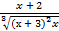

= = = – .

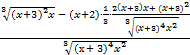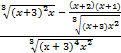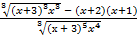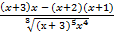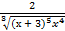Точками, подозрительными на перегиб (там, где вторая производная y²(x) равна нулю или не существует) являются точки x₁ = –3; x₃ = 0. В данном случае точки, в которых y²(x) = 0, отсутствуют.

В области –¥ < x < –3 вторая производная y² > 0 и функция y = f(x) выпукла вниз (вогнута). В области –3 < x < 0 вторая производная y² < 0 и функция y = f(x) выпукла вверх (выпукла). В области 0 < x < +¥ вторая производная y² < 0 и функция y = f(x) также выпукла вверх. Так как в точке x₁ = –3 вторая производная y² меняет знак с «+» на «–», то точка x₁ является точкой перегиба.

6. Найдем наклонные (горизонтальные) асимптоты графика функции; как указано выше, вертикальных асимптот график функции y(x) не имеет. Как известно, наклонная асимптота имеет вид y = kx + b, коэффициенты k и b которой могут быть найдены как пределы:

k = 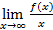; b = .

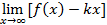В данном случае,

k = 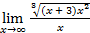= = 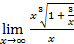= 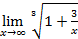1;

b = = {¥ – ¥} = = = .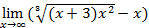

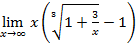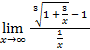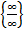Для вычисления последнего предела удобно сделать замену переменной t = . При x ® ¥ новая переменная t ® 0. Теперь, используя правило Лопиталя, имеем окончательно

b = 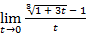= = 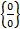= = 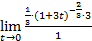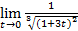1.

Таким образом, график y(x) исследуемой функции имеет единственную наклонную асимптоту y = x + 1.

7. Необходимости в дополнительных вычислениях для уточнения поведения графика функции y(x) нет. Можно, однако, заметить дополнительно, что y(x) < 0 при x < –3; при x > –3, напротив, y(x) > 0.

8. Объединяя результаты проведенных выше исследований, строим график функции y = f(x) (рис. 2).

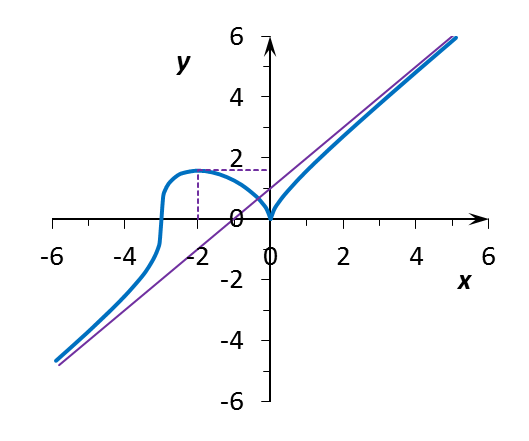
Рис. 2

б) Проведем полное исследование функции y = f(x) = 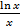– x, как и прежде придерживаясь рекомендуемой схемы.

1. Функция f(x) определена для всех действительных x > 0, т.е. D = (0; +¥).

2. Функция не имеет точек разрыва, т.е. является непрерывной всюду на области D своего определения, однако, при x ® 0 + 0 f(x) ® – ¥. Линия x = 0, т.е. ось Oy, является вертикальной асимптотой графика y(x). Для нахождения нулей функции y = f(x) следует решить уравнение

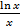– x = 0,

или

ln x = x².

Это уравнение не имеет действительных корней. Для того, чтобы убедиться в этом, достаточно сопоставить два графика элементарных функций y = ln x и y = x².

3. Функция f(x) не является четной или нечетной, не является периодической, т.е. является функцией общего вида.

4. Для исследования функции на монотонность и экстремум вычислим ее первую производную:

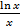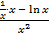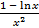y¢ = ( – x)¢ = – 1 = – 1 = .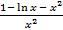

Особыми точками являются: точка x₀ = 0 (при x ® 0 производная функции y¢(x) ® +¥) и точка x₁ = 1 (здесь y¢(x) = 0). В первом случае, очевидно, имеем вертикальную асимптоту x = 0 для графика функции y(x). Во втором случае, как нетрудно видеть, сравнив графики элементарных функций y = ln x и y = 1 – x², уравнение

ln x = 1 – x²

имеет единственным корнем именно x₁ = 1. Заметим, что при x < 1 ln x < 1 – x², а при x > 1 ln x > 1 – x².

Особые точки делят область определения функции D на два (непересекающихся) интервала: D₁ = (0; 1) и D₂ = (1; +¥). Изучим каждый из них.

Интервал D₁ = (0; 1). Здесь y¢ > 0 и функция y = f(x) возрастает.

Интервал D₂ = (1; +¥). Здесь y¢ < 0 и функция y = f(x) убывает.

Знак первой производной y¢(x) изменяется c «+» на «–» в точке x₁ = 1; в этой точке функция y = f(x) достигает (локального) максимума, равного y_max = f(1) = –1.

5. Для определения интервалов выпуклости и вогнутости и точек перегиба вычислим вторую производную функции, как производную отношения:

y² = ( 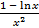– 1)¢ = = .

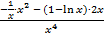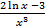Точками, подозрительными на перегиб (там, где вторая производная y²(x) равна нулю или не существует) являются точки x₀ = 0 и x₂ = e^3/2 » 4,482.

В области 0 < x < x₂ вторая производная y² < 0 и функция y = f(x) выпукла вверх (выпукла). В области x₂ < x < +¥ вторая производная y² > 0 и функция y = f(x) выпукла вниз (вогнута). Так как в точке x₂ = e^3/2 » 4,482 вторая производная y² меняет знак с «–» на «+», то точка x₂ является точкой перегиба.

6. Найдем наклонные (горизонтальные) асимптоты y = kx + b графика функции. В данном случае, применяя правило Лопиталя, находим

k 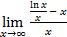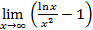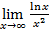= = = – 1 + = –1,

действительно, 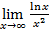= = 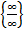= 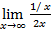0.

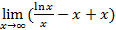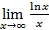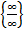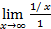b = = = = = 0.

Таким образом, график y(x) исследуемой функции имеет единственную наклонную асимптоту y = –x.

7. Необходимости в дополнительных вычислениях для уточнения поведения графика функции y(x) нет. Можно, однако, заметить дополнительно, что разность между значениями исследуемой функции y(x) = 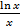– x и соответствующими асимптотическими значениями y = –x всегда положительна: Dy(x) = 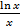– x – (–x) = 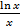> 0 при x > 0. Поэтому функция y = f(x) приближается к своей асимптоте сверху.

8. Объединяя результаты проведенных выше исследований, строим график функции y = f(x) (рис. 3).

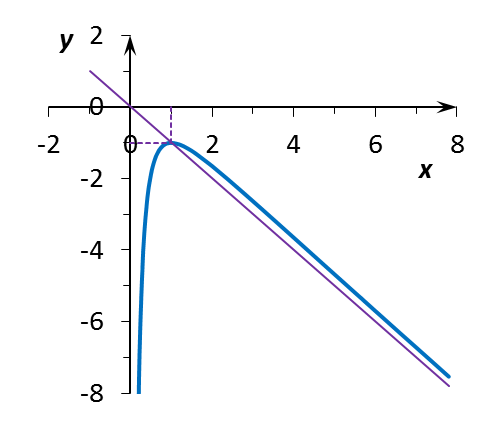
Рис. 3