ИДЗ-12. Решение задачи оптимизации. Построить математическую модель и решить задачу оптимизации.
Построить математическую модель и решить задачу оптимизации.
Среди всех равнобедренных треугольников с заданным периметром p найти треугольник наибольшей площади. Чему она равна?
| A |
необходимые обозначения в рассматриваемом треугольнике DABC: AB = AC = x; BC = y; AD = x×cosa; ÐA = 2a. Заданный периметр p = 2x + y.
Из геометрических соображений имеем:
| a |
| a |
p = 2x + 2x sin a = 2x (1 + sin a),
| C |
| D |
| B |
x =  ×
× 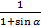 .
.
| Рис. 4 |
S =  ×BC×AD =
×BC×AD =  ×2x sin a×x cosa =
×2x sin a×x cosa =  ×x2 sin 2a =
×x2 sin 2a = 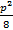 ×
× 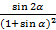 .
.
Ясно, что 0 £ a £  . Остается найти максимальное значение целевой функции:
. Остается найти максимальное значение целевой функции:
f(a) = 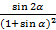 .
.
Для этого вычислим производную функции f(a) и приравняем ее нулю:
f¢(a) = 0 = ( 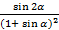 )¢ =
)¢ = 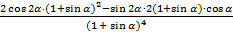 = 2×
= 2× 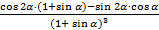 =
=
= 2× 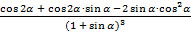 = 2×
= 2× 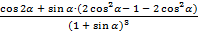 = 2×
= 2× 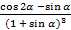 .
.
При допустимых значениях угла a выражение 1 + sin a > 0, так что f¢(a) = 0 при
cos 2a – sin a = 0;
1 – 2sin2 a – sin a = 0;
2sin2 a + sin a – 1 = 0;
D = 12 – 4×2×(–1) = 9;
sin a = 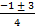 =
= 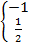 ;
;
Допустимым значениям угла a отвечает лишь решение sin a = ½, откуда a0 =  и ÐA =
и ÐA =  . Тогда y = 2x×
. Тогда y = 2x×  = x, т.е. DABC равносторонний.
= x, т.е. DABC равносторонний.
Нетрудно (СРС) вычислить вторую производную целевой функции f(a):
f²(a) = (2× 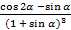 )¢ = –2×
)¢ = –2× 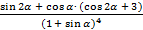 .
.
При найденном значении am =  вторая производная f²(a0) < 0, т.е. в точке am =
вторая производная f²(a0) < 0, т.е. в точке am =  площадь S(a) достигает именно максимума, равного
площадь S(a) достигает именно максимума, равного
Sm = S(  ) =
) = 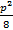 ×
× 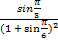 =
= 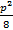 ×
× 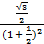 =
= 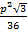 .
.
Ответ: am =  ; Sm =
; Sm = 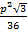 .
.
Варианты индивидуальных домашних заданий (ИДЗ) по Математике
Дата добавления: 2014-12-06; просмотров: 2118;
