ИДЗ-9. Вычисление производных. а) Найти y¢ и y²; б) для данной функции y(x) и точки x0 вычислить y²¢(x0):

а) Найти y¢ и y²; б) для данной функции y(x) и точки x₀ вычислить y²¢(x₀):

а) x³y – y² = 6x; б) y = ⅛ – ¼ cos²x, x₀ = p/4.

Решение: а) Продифференцируем по x обе части равенства:

(x³y)¢ – (y²)¢ = (6x)¢;

3x²y + x³y¢ – 2yy¢ = 6,

откуда

y¢ = .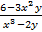

Продифференцируем по x обе части равенства 3x²y + x³y¢ – 2yy¢ = 6 еще раз:

(3x²y)¢ + (x³y¢)¢ – (2yy¢)¢ = (6)¢;

6xy + 3x²y¢ + 3x²y¢ + x³y¢¢ – 2y¢²– 2yy² = 0,

откуда

y²(x³ – 2y) = 2y¢² – 6x²y¢ – 6xy.

Подставляя теперь вместо y¢ полученное выше выражение, имеем окончательно:

y² = 2× 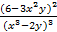– 6x²× – .

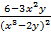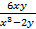б) Продифференцируем последовательно данную функцию y(x):

y¢ = (⅛ – ¼ cos²x)¢ = –¼×2×cos x×(–sin x) = ¼×sin 2x;

y² = (¼×sin 2x)¢ = ¼×2×cos 2x = ½×cos 2x;

y²¢ = (½×cos 2x)¢ = –½×2×sin 2x = –sin 2x.

Теперь легко получаем: y²¢(x₀ = p/4) = –sin(2×p/4) = –sin(p/2) = –1.

Ответ: y²¢ = –sin 2x; y²¢(x₀ = p/4) = –1.