Вычисление длины дуги кривой

y y = f(x)

DS_i Dy_i

Dx_i

a b x

Длина ломаной линии, которая соответствует дуге, может быть найдена как .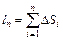

Тогда длина дуги равна .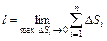

Из геометрических соображений: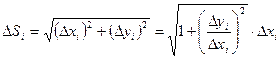

В то же время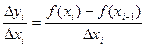

Тогда можно показать, что

.

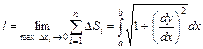Т.е. .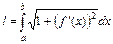

Если уравнение кривой задано параметрически, то с учетом правил вычисления производной параметрически заданной функции, получаем

,

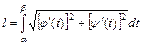Если кривая задана в полярных координатах, то

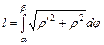, r = f(j).

Пример. Найти длину окружности, заданной уравнением x² + y² = r².

Решение.Выразим из уравнения переменную у: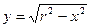

Найдем производную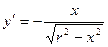

Тогда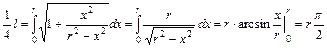

Тогда l = 2pr. Получили общеизвестную формулу длины окружности.

Вопросыдля самопроверки

1. Что называется интегральной суммой данной функции f(x) на данном отрезке

[а, b]?

1. Дайте определение определенного интеграла.
2. Каков геометрический смысл определенного интеграла от данной функции?
3. Перечислите основные свойства определенного интеграла.
4. Напишите формулу Ньютона — Лейбница.
5. В чем состоит способ подстановки для вычисления определенного интеграла?
6. Как выглядит формула интегрирования по частям дляопределенного интеграла?
7. Как вычислить площадь криволинейного сектора в полярных координатах?
8. Запишите формулы для вычисления длины дуги кривой в декартовых и в полярных координатах.
9. Приведите формулу для вычисления объема тела с известными площадями его поперечных сечений.
10. Запишите формулу для вычисления объема тела вращения.

Тема 6. Дифференциальные уравнения

Литература: [1], [2], [3], [4], [6], [8], [12], [18], [19], [20], [21], [22].