Однородные дифференциальные уравнения первого порядка. Уравнение первого порядка называется однородным, если f(x,y) можно представить как функцию только одного отношения переменных

Уравнение первого порядка называется однородным, если f(x,y) можно представить как функцию только одного отношения переменных , т.е. уравнение вида 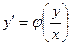. Однородное уравнение приводится к уравнению с разделяющимися переменными посредством замены функции у (или х) новой функцией t по формуле y=tx (x=ty), причем .

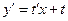Пример. Найти общий интеграл дифференциального уравнения

.

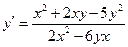Решение. Данное уравнение первого порядка уже разрешено относительно производной. Установим, что она является функцией только отношения переменных , т.е. установим, что данное уравнение является однородным. Для этого числитель и знаменатель дроби разделим на x². (Другими словами, сократим дробь на x².)

.

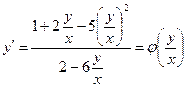Далее вводим новую функцию 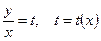. Отсюда, . После подстановки данное уравнение преобразуется в уравнение с разделяющимися переменными . Разделим переменные: 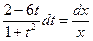и, интегрируя, найдем

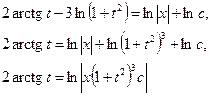
Возвращаясь к старым переменным, получим

Ответ: .