Решение линейных уравнений первого порядка с помощью подстановки

Уравнение (3) можно решить с помощью подстановки: y=UV, где U=U(x), V=V(x). Тогда .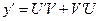

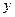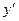Подставим и в (3):

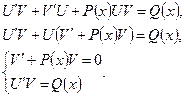
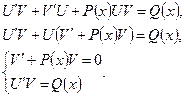
Во многих примерах необходимо решить задачу Коши. Процесс решения сводится к отысканию частного интеграла дифференциального уравнения n-го порядка (n=1,2,3,...), удовлетворяющего n начальным условиям вида

.

.

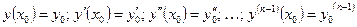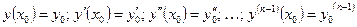Т.е. ищут общее решение дифференциального уравнения, а затем, воспользовавшись начальными условиями, находят значения всех n произвольных постоянных c₁, c₂,..., c_n, входящих в общий интеграл уравнения.

Пример. Найти решение задачи Коши:

.

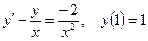Решение. Перед нами линейное дифференциальное уравнение 1-го порядка. Решим его двумя способами.

I-способ. Решение уравнения ищется в виде произведения двух функций U=U(X) и V=V(X), т.е. y=UV, одна из которых выбирается произвольным образом; 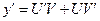. Подставляя в исходное уравнение, получим

.

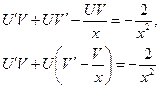Исходя из того, что одну из функций ищут произвольным образом, полученное уравнение разбивают на два следующим способом:

.

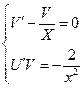Выпишем первое уравнение из системы и решим его:

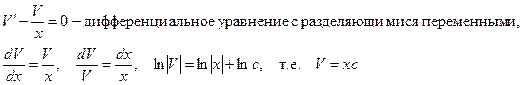
Мы можем воспользоваться частным случаем функции V, например, когда c=1, V=x (значение для c берут таким образом, чтобы функция V не оказалась тождественно равной нулю, в противном случае невозможно будет искать функцию U). Подставим найденное значение для V во второе уравнение системы и найдем функцию U: .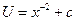

Следовательно, функция 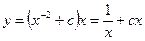. Таким образом, найдено общее решение исходного уравнения. Подставляя начальное условие, найдем c: c=0.

Т.е. решением задачи Коши, удовлетворяющем данному начальному условию является 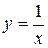, что и будет ответом.

II-способ. Метод вариации произвольной постоянной.

Составим и решим соответствующее однородное уравнение:

.

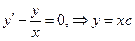Теперь предположим, что константа c является функцией от переменной x, т.е. c=c(x), тогда y=xc(x). Найдем 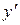и подставим в исходное уравнение:

.

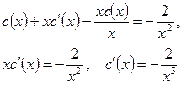Интегрируя обе части уравнения, получим

.

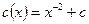Тогда 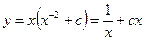- общее решение исходного дифференциального уравнения. Подставляя начальное условие, найдем, что c=0 и 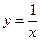- частное решение.