Признаки сходимости рядов с положительными членами
Признак Даламбера. Если для знакоположительного ряда 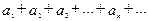 существует
существует
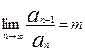 , (5)
, (5)
то при 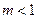 ряд сходится, при
ряд сходится, при  ряд расходится; при
ряд расходится; при 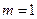 вопрос о сходимости ряда остается открытым (в этом случае необходимо применять другие признаки сходимости рядов).
вопрос о сходимости ряда остается открытым (в этом случае необходимо применять другие признаки сходимости рядов).
Признак Коши.Если существует
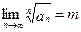 , (6)
, (6)
то при 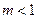 ряд
ряд 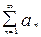 ,
, 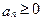 , сходится; при
, сходится; при  – расходится, при
– расходится, при 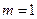 ряд может сходиться или расходиться (требуется дополнительное исследование).
ряд может сходиться или расходиться (требуется дополнительное исследование).
Интегральный признак Коши.Если функция  непрерывная, положительная, не возрастающая для
непрерывная, положительная, не возрастающая для 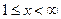 и при натуральных значениях аргумента x
и при натуральных значениях аргумента x
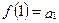 ,
, 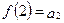 , ...,
, ..., 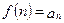 ,...,
,...,
то ряд 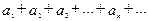 и несобственный интеграл
и несобственный интеграл 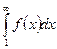 одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
Пример. Исследовать на сходимость ряд 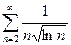 :
:
a) с помощью признака Даламбера;
b) используя интегральный признак.
Решение.
a) По условию,  ,
, 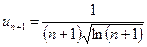 , следовательно,
, следовательно,
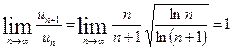 ,
,
т.е. признак Даламбера не позволяет сделать заключения о сходимости или расходимости ряда.
b) Члены данного ряда положительны и убывают; в качестве функции  возьмем функцию
возьмем функцию 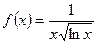 при
при  ; эта функция непрерывна и убывает, причем
; эта функция непрерывна и убывает, причем 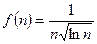 . Так как
. Так как
 ,
,
то данный ряд расходится.
Дата добавления: 2014-12-05; просмотров: 1230;
