Знакопеременные ряды

Определение. Числовые ряды, члены которых как положительные числа, так и отрицательные, называются знакопеременными.

Знакочередующиеся ряды

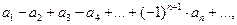
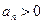
являются частным случаем рядов знакопеременных.

Определение. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится, то данный знакопеременный ряд называется условно или неабсолютно сходящимся.

Теорема.Если сходится ряд, составленный из абсолютных величин членов данного ряда, то сходится и данный ряд, называемый в этом случае абсолютно сходящимся.

Теорема Лейбница (достаточный признак сходимости знакочередующегося ряда) Если абсолютные величины членов знакочередующегося ряда 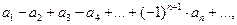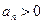, монотонно убывают и абсолютная величина общего члена ряда стремится к нулю при 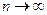, то ряд сходится, его сумма положительна и меньше первого члена.

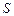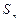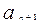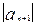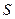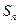Следствие. При замене суммы ряда частичной суммой мы отбрасываем все члены ряда начиная с , т.е. отбрасываем знакочередующийся ряд, который удовлетворяет признаку Лейбница. Сумма этого ряда по абсолютной величине меньше модуля первого члена ряда, т.е. меньше . Значит, абсолютная величина допущенной ошибки при такой замене на будет меньше абсолютной величины первого члена отброшенной части ряда.

Пример. Исследовать на сходимость ряд .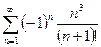

Решение. Этот ряд знакопеременный. Исследуем его на абсолютную сходимость. Составляя ряд из абсолютных величин (модулей) членов данного ряда, получим ряд

.

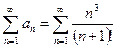Применим признак Даламбера. Выпишем члены 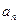и :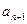

, .

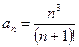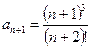Тогда 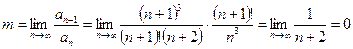, , 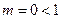т.е. ряд 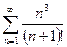сходится. Следовательно, исходный ряд 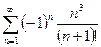сходится абсолютно.

Вопросы для самопроверки

1. Дайте определения сходящегося и расходящегося рядов. Исследуйте сходимость ряда, составленного из членов геометрической прогрессии.
2. Докажите необходимый признак сходимости ряда.
3. Докажите, что отбрасывание конечного числа членов ряда не изменяет его сходимости (расходимости). Покажите, что сумма ряда равна сумме его первых n членов, сложенной с сумой ряда, полученного из данного отбрасыванием этих n членов.
4. Докажите теорему о сравнении рядов с положительным членами. Приведите пример применения этого признака.
5. Докажите признак Даламбера сходимости знакопеременных рядов. Приведите пример применения этого признака.
6. Докажите признак Коши сходимости рядов с положительными членами. Приведите пример применения этого признака.
7. Докажите интегральный признак Коши сходимости ряда. Приведите пример применения этого признака.
8. Дайте определение абсолютно сходящегося ряда. Докажите, что из абсолютной сходимости ряда следует его сходимость. Сформулируйте свойства абсолютно сходящихся рядов. Приведите пример абсолютно и условно сходящихся рядов.
9. Докажите признак Лейбница сходимости знакочередующихся рядов. Приведите пример на применение этого признака. Покажите, что при замене суммы ряда типа Лейбница суммой первых его членов допускаемая абсолютная погрешность не превосходит модуля первого отброшенного члена.