Знакопеременные ряды. Ряд члены которого могут иметь произвольные знаки, называется знакопеременным рядом.

Ряд члены которого могут иметь произвольные знаки, называется знакопеременным рядом.

Для знакопеременного ряда

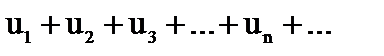(1)

будем рассматривать ряд, составленный из абсолютных величин его членов

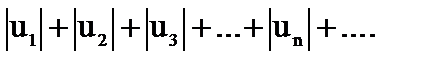(2)

Ряд (2) является рядом с положительными членами, признаки сходимости таких рядов изложены выше.

Рассмотрим без доказательства признак сходимости знакопеременных рядов.

Если ряд (2), составленный из абсолютных величин членов ряда (1) сходится, то ряд (1) также сходится.

Пример 1. Рассмотрим ряд

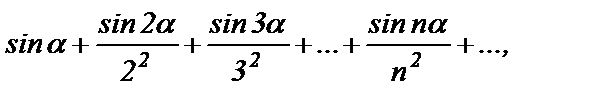(3)

где 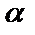- произвольное число. Понятно, что (3) – знакопеременный ряд. Исследуем ряд из абсолютных величин

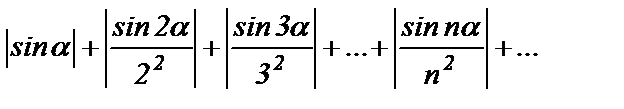(4)

Докажем, что он сходится, сравнив его со сходящимся рядом

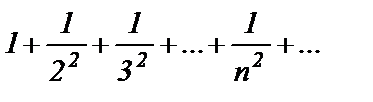
(вспомните 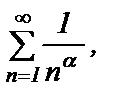который сходится при ).

Т.к. всегда 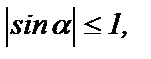то

Поскольку ряд (4) из абсолютных величин сходится, то сходится и данный ряд (3) .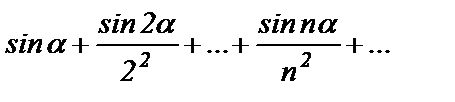

Все сходящиеся знакопеременные ряды делятся на абсолютно и условно сходящиеся.